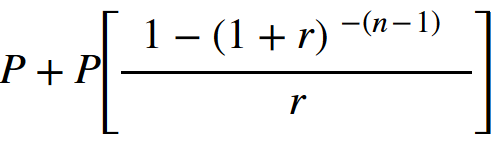• Present Value (PV)

The present value formula refers to the application of the time value of money that discounts the future cash flow to arrive at its present-day value. PV=FV(1+r%)n Where, PV = Present value FV = Future value r = Rate of interest (percentage ÷ 100) n = Number of times the amount is compounding The value of n varies depending on the number of times the amount is compounding. n = 1, if the amount is compounded yearly. n = 2, if the amount is compounded half-yearly. n = 4, if the amount is compounded quart-yearly. n = 12, if the amount is compounded monthly. n = 52, if the amount is compounded weekly. n = 365, if the amount is compounded daily.

 

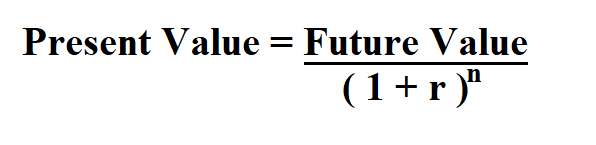
• PV Factor

The present value interest factor (PVIF) is a formula used to estimate the current worth of a sum of money that is to be received at some future date. PVIFs are often presented in the form of a table with values for different time periods and interest rate combinations.

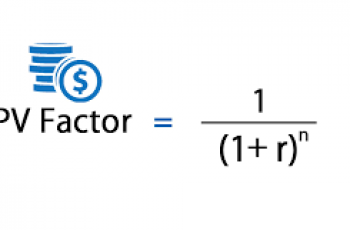
• PV Annuity

The present value of an annuity refers to how much money would be needed today to fund a series of future annuity payments

• PV Annuity factor

The present value annuity factor is used to calculate the present value of future one dollar cash flows. The present value of annuity formula determines the value of a series of future periodic payments at a given time. The present value of annuity formula relies on the concept of time value of money, in that one dollar present day is worth more than that same dollar at a future date.

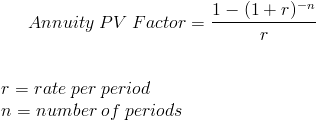
• PV Annuity due

The formula for the present value of an annuity due, sometimes referred to as an immediate annuity, is used to calculate a series of periodic payments, or cash flows, that start immediately.

 

• PV Stock at Zero growth

The formula for the present value of a stock with zero growth is dividends per period divided by the required return per period. The present value of stock formulas are not to be considered an exact or guaranteed approach to valuing a stock but is a more theoretical approach.

 

 

 

 

 

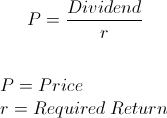
• PV Stock at Constant growth

The formula for the present value of a stock with constant growth is the estimated dividends to be paid divided by the difference between the required rate of return and the growth rate. The present value of a stock with constant growth is one of the formulas used in the dividend discount model, specifically relating to stocks that the theory assumes will grow perpetually. The dividend discount model is one method used for valuing stocks based on the present value of future cash flows, or earnings.

• PV Growing perpetuity

The present value of a growing perpetuity formula is the cash flow after the first period divided by the difference between the discount rate and the growth rate.

 

• PV Growing annuity

The present value of a growing perpetuity formula is the cash flow after the first period divided by the difference between the discount rate and the growth rate. It is important to note that the discount rate must be higher than the growth rate when using the present value of a growing perpetuity formula. This is due to the present value of a growing perpetuity formula being an infinite geometric series as explained in one of the following sections. In theory, if the growth rate is higher than the discount rate, the growing perpetuity would have an infinite value.

 

• PV compounding

The present value formula consists of the present value and future value related to compound interest. The present value or PV is the initial amount (the amount invested, the amount lent, the amount borrowed, etc). The future value or FV is the final amount. i.e., FV = PV + interest.

 

 

References

Pattavina, J. (2018). The Time-Value of Money.

Stephen, D. Lindon J. (2017) Financial management for small Businesses.

Pamela, P. Frank, J (2009) Foundation and Application of Time Value of Money

Michael, T.(2012) Corporate Finance For Dummies

Johan M. (2004) Financial Calculator For Time Value of Money