TABLE OF CONTENTS

• Introduction
• Calculator use
• Conical frustum formulas
• Types of frustums
• Properties of a frustum
• Net of a frustum
• References

Introduction

In geometry, a frustum is the portion of a solid that lies between two parallel planes cutting this solid. In the case of a pyramid, the base faces are polygonal while the side faces are trapezoidal. A right frustum is a right pyramid or a right cone truncated perpendicularly to its axis, otherwise it is an oblique frustum. A frustum's axis is that of the original cone or pyramid. The height of a frustum is the perpendicular distance between the planes of the two bases. Cones and pyramids can be viewed as degenerate cases of frusta, where one of the cutting planes passes through the apex.

 

Definition of Frustum-A frustum can be defined as a solid shape obtained from cutting a cone or a pyramid from top. It is that section of the cone or pyramid which lies between the base and the plane parallel to the base. It is a 3D figure obtained from other 3D figures such as a cone or pyramid.

 

 

 

 

  

 

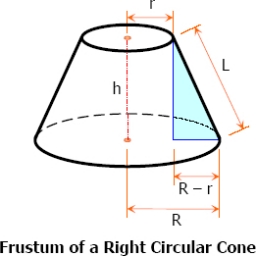
Fig 1.1

 

r = radius1
R= radius2
h = height
L = slant height
 

Calculator Use

This calculator will calculate the various properties of a conical frustum given the 2 radii and any 1 other known variable. This geometric solid conical frustum is a type of right circular cone, where a right cone is a cone with its vertex point above the center of its base. The frustum is a cone with the top cut off by making a slice parallel to the base.

Conical Frustum Formulas

• Volume of a conical frustum:

       V = (1/3) * π * h * (r² + R² + (r * R))

•  volume of a pyramid frustum(polygon based):

       V =  n*h/12*(b2+b.B+B2)*cot(3.142/n)

• surface area of a conical frustum:

       A=π * (r² + R² + (r + R) * L)

• Total surface area of a conical frustum:

       A = π * (r² + R² + (r + R) * L) = π * [ r² + R² + (r + R) * √((r1- R)2 + h2) ]

Types of Frustums

There exists two types of frustum namely cone frustum and pyramid frustum.

A cone frustum: Created by cutting the cone from the vertex or apex. A plane parallel to the base of the cone cuts the top of the cone or the apex to create a frustum. It is also called a frustum of a cone or truncated cone.

A pyramid frustum: Formed by cutting the apex of the pyramid with a plane parallel to the base. Here, the pyramid's base can either be a triangle or a square. Hence, frustum can be created from triangular pyramids and square pyramids.

Below is a diagrammatic representation of both.

 

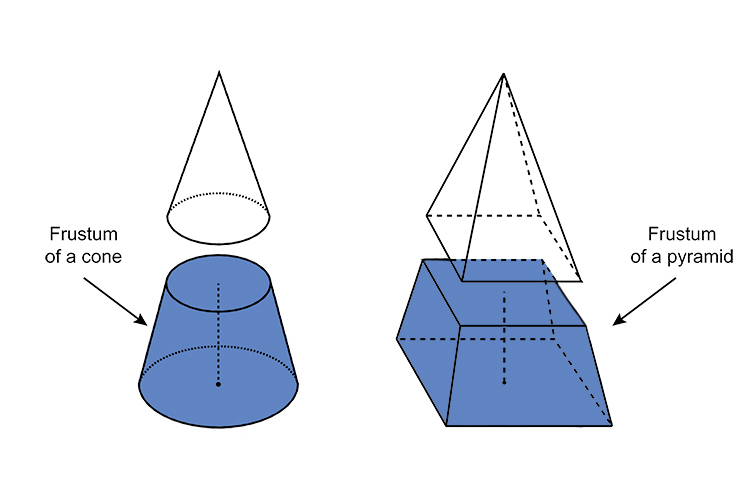
Fig. 1.2

Properties of a Frustum

•         A frustum can be determined by the height of the solid figure that remained after cutting off a cone or pyramid.
•        Its radius can be determined by calculating the radius of both the bases i.e. the top and bottom.
•        The plane part of the frustum is called the floor.
•        If we find an axis of a frustum, it is mostly the axis of the cone or pyramid (the original shape).
•        If the axis is perpendicular to the base, then the frustum is a right frustum otherwise it is an oblique frustum.
•        A frustum can have a triangle and square-shaped base if a triangular pyramid and a square pyramid are cut off from the apex.

 

Net of a frustum

When a pyramid or a cone is cut off by using a plane that is parallel to its base, the solid structure left behind is called a frustum. The net of a frustum is formed by a shape similar to a cylinder and two circles - one small in size and the other one is bigger in size. 

Below is an image of a frustum net for a cone.

Fig. 1.3

 

References

https://www.cuemath.com/geometry/frustum/

https://math.fandom.com/wiki/Frustum

https://www.calculatorsoup.com/calculators/geometry-solids/conicalfrustum.php