Loan Interest Calculator is used to calculate the price one pays to borrow money from someone else. The calculator is the remedy for performing quick computations to determine the interest on any amount of loan issued.
This page gives a detailed information covering everything on the calculator:
Introduction
When you borrow money, you are expected to pay back the funds over time. However, lenders expect to be paid something for their services and the risk they take when lending you money. That means you won’t just pay back the money you borrowed. You’ll pay back the loan plus an additional sum, called interest.
Description of the Calc
This calculator will allow you to enter ANY FIVE of these and calculate the sixth: 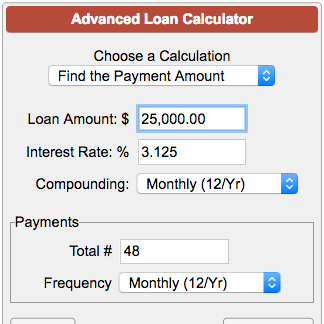
(a) the annual interest rate
(b) the number of periods in the year
(c) the number of years
(d) the starting balance (negative for loans and positive for investments)
(e) your monthly payment
(f) the final balance.
This calculator will permit you to :
Get mortgage loans setting (f) the final balance to zero and calculate (e) your monthly payment.
Know Credit Card repayments by setting (f) the final balance to zero and calculate (c) the number of years it will take to pay off the balance.
Calculate saving plans by literally setting (d) the starting balance to zero and calculate (f) the final balance.
Understand investments by having the monthly repayment set to zero and calculate (f) the final balance.
How to calculate loan interest
To maximize profits, lenders take different approaches when it comes to charging interest. There are two ways one can obtain the interest on a loan thus using;
Simple interest
Compound interest
1. Simple Interest
If a lender uses the simple interest method, it’s easy to calculate loan interest if you have the right information available. Gather information like your principal loan amount, interest rate and a total number of months or years that you’ll be paying the loan. It is calculated by the formula ;S.I. = (P × T × R) ⁄ 100.
2. Compound interest
total amount of principal and interest in future (or future value) less principal amount at present (or present value)
= [P (1 + i)n] – P
= P [(1 + i)n – 1]
Where:
P = principal
i = nominal annual interest rate in percentage terms
n = number of compounding periods
Examples
Simple interest
Enter your values here
Mark deposits $4,000 at a bank at an interest rate of 4.5% per year. How much interest will she earn at the end of 3 years?
Solution:
Simple Interest = 4,000 × 4.5% × 3 = 540
She earns $540 at the end of 3 years.
Compound Interest
Use this to make calculations:
A principal of $2000 is placed in a savings account at 3% per annum compounded annually. How much is in the account after one year, two years and three years?
Solution
When interest is compounded annually, total amount A after t years is given by: A = P(1 + r) t, where P is the initial amount (principal), r is the rate and t is time in years.
1 year: A = 2000(1 + 0.03) 1 = $2060
2 years: A = 2000(1 + 0.03) 2 = $2121.80
3 years: A = 2000(1 + 0.03) 3 = $2185.45
Algorithm
1. Apply the following algorithm in simple interest:
def P = #P
def i = #i
def n = #n
BigDecimal d = P*(1+(n*i))
return d.setScale(2, BigDecimal.ROUND_HALF_EVEN)
2. Apply this algorithm for Compound Interest
def p=#p
def r=#r
def n=#n
def t=#t
def a = p*((1+(r/n))**(n*t))
return a
References
https://www.bankrate.com/loans/personal-loans/how-to-calculate-loan-interest/
https://www.investopedia.com/terms/c/compoundinterest.asp