This calculator gives you the ability to calculate the length of one of the sides of a right triangle, given the length of the other two sides.

Description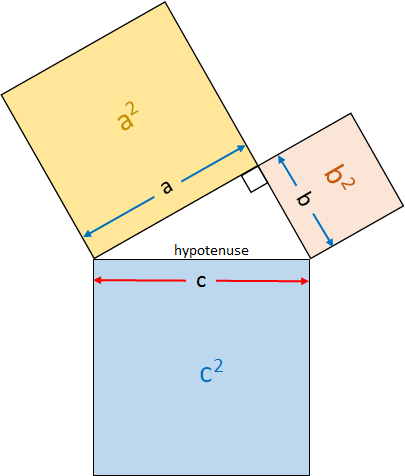

In mathematics, the Pythagorean theorem, or Pythagoras' theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides a, b and c, often called the Pythagorean equation:[1]

(a² +b² =c²    )

where c represents the length of the hypotenuse and a and b the lengths of the triangle's other two sides. The theorem, whose history is the subject of much debate, is named for the Greek philosopher Pythagoras, born around 570 BC.

The theorem has been proven numerous times by many different methods - possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years.

The theorem can be generalized in various ways: to higher-dimensional spaces, to spaces that are not Euclidean, to objects that are not right triangles, and to objects that are not triangles at all but n-dimensional solids. The Pythagorean theorem has attracted interest outside mathematics as a symbol of mathematical abstruseness, mystique, or intellectual power; popular references in literature, plays, musicals, songs, stamps, and cartoons abound.

Other forms of the theorem

If c denotes the length of the hypotenuse and a and b denote the lengths of the other two sides, the Pythagorean theorem can be expressed as the Pythagorean equation:

 a²+b²=c²

If the lengths of both a and b are known, then c can be calculated as

c =√a²+b² 

If the length of the hypotenuse c and of one side (a or b) are known, then the length of the other side can be calculated as

 a=√ c²-b²   

or

 b=√c²-a²         click here

The Pythagorean equation relates the sides of a right triangle in a simple way, so that if the lengths of any two sides are known the length of the third side can be found. Another corollary of the theorem is that in any right triangle, the hypotenuse is greater than any one of the other sides, but less than their sum.

Usage

Because we live in a world where the geometry of gravity paints right triangles on everything, the Pythagorean theorem is central to an innumerable set of equations that describe phenomena we see and feel every day.  Objects rolling or sliding down a plane are moving down the hypotenuse of a right triangle formed with the local horizontal plane and the vector of gravity. The pendulum motion of a swinging wrecking ball translates its component forces into a right triangle with one side of the triangle being the force of gravity. The shadow cast from a tree or a building forms a right triangle with the distance from the foot of the building.

APPLICATION OF PYTHAGOREAN THEOREM IN REAL LIFE

Architecture and Construction

Given two straight lines, the Pythagorean Theorem allows you to calculate the length of the diagonal connecting them. This application is frequently used in architecture, woodworking, or other physical construction projects. For instance, say you are building a sloped roof. If you know the height of the roof and the length for it to cover, you can use the Pythagorean Theorem to find the diagonal length of the roof's slope. You can use this information to cut properly sized beams to support the roof, or calculate the area of the roof that you would need to shingle.

Laying Out Square Angles

The Pythagorean Theorem is also used in construction to make sure buildings are square. A triangle whose side lengths correspond with the Pythagorean Theorem – such as a 3 foot by 4 foot by 5 foot triangle – will always be a right triangle. When laying out a foundation, or constructing a square corner between two walls, construction workers will set out a triangle from three strings that correspond with these lengths. If the string lengths were measured correctly, the corner opposite the triangle's hypotenuse will be a right angle, so the builders will know they are constructing their walls or foundations on the right lines.

Navigation

The Pythagorean Theorem is useful for two-dimensional navigation. You can use it and two lengths to find the shortest distance. For instance, if you are at sea and navigating to a point that is 300 miles north and 400 miles west, you can use the theorem to find the distance from your ship to that point and calculate how many degrees to the west of north you would need to follow to reach that point. The distances north and west will be the two legs of the triangle, and the shortest line connecting them will be the diagonal. The same principles can be used for air navigation. For instance, a plane can use its height above the ground and its distance from the destination airport to find the correct place to begin a descent to that airport.

Surveying

Surveying is the process by which cartographers calculate the numerical distances and heights between different points before creating a map. Because terrain is often uneven, surveyors must find ways to take measurements of distance in a systematic way. The Pythagorean Theorem is used to calculate the steepness of slopes of hills or mountains. A surveyor looks through a telescope toward a measuring stick a fixed distance away, so that the telescope's line of sight and the measuring stick form a right angle. Since the surveyor knows both the height of the measuring stick and the horizontal distance of the stick from the telescope, he can then use the theorem to find the length of the slope that covers that distance, and from that length, determine how steep it is.

See also

Pythagorean Theorem [multiple proofs]

Square Root of Two - common case where sides adjacent to hypotenuse are both of length 1.

Pythagorean Theorem - Khan Academy video

1. ^ http://en.wikipedia.org/wiki/Pythagorean_theorem