Importance of Solar Panel Pointing

This page discusses why it is important to point the face of the solar panel as much as possible directly at the Sun.  Think of the light coming from the Sun to the Earth across 93 million miles as an arrow.  That arrow points to the surface of the Earth near you at a different angles throughout each day.  Near dawn and nightfall the Sun is low on the horizon and light is coming to the surface at a very low angle.  Near midday the Sun is at its highest point and the angle of the sunlight hitting the Earth is a much steeper angle.  The angle at which the imagined arrow of sunlight strikes the Earth Surface is the incidence angle.

When the Sun's rays are perpendicular to an absorbing surface, the light on that surface has the highest possible power density. In other word's, if the face of a surface which can absorb the Sun's energy is directly facing the Sun, that surface will absorb the most energy from the Sun possible. The incidence angle of 90% from the the absorbing surface provides maximum energy.

As the angle between the sunlight (the arrow we imagined from the Sun to us) and the absorbing surface changes, the intensity of light on the surface is reduced. The extreme case where the surface is parallel to the sun's rays illustrates this best.  The intensity of light falls to zero when the sunlight travels parallel to the absorbing surface.  This is the intuitive case, as we can imagine the light rays from the sun (our imagined arrow) is passing right by the absorbing surface, not striking the surface and therefore not imparting energy to the surface.

The figure below illustrates three cases for the incidence angle of sunlight: 

• 90 degrees which will impart the maximum solar energy to the absorbing surface
• less than 90 degreed, which will impart solar energy that will vary with the sine of the incidence angle
• 0 degrees, which will impart no energy to the solar surface

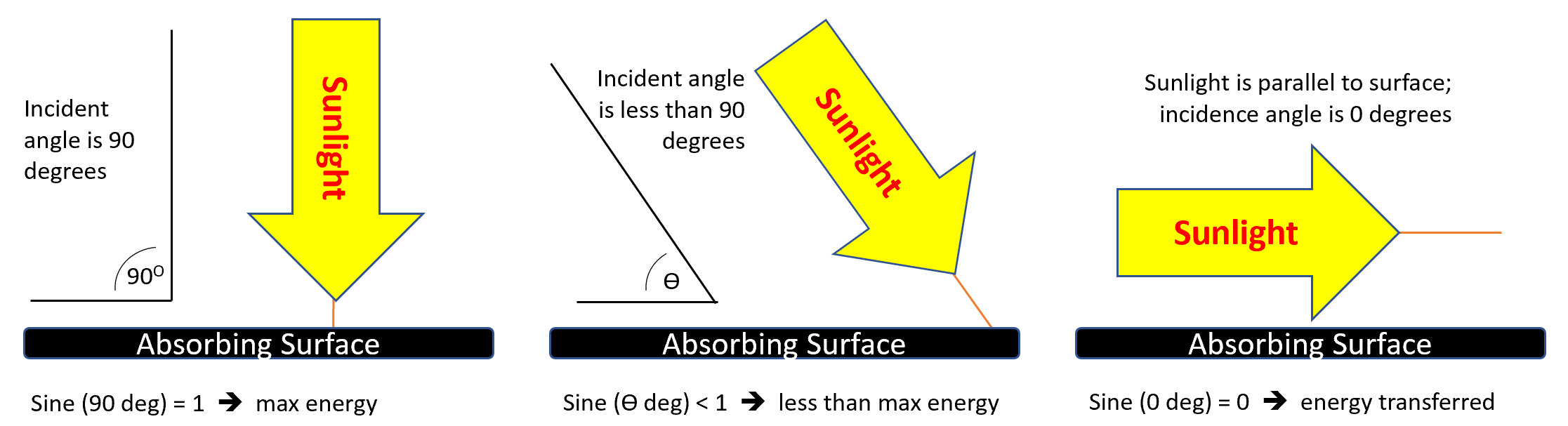
Figure: Solar Incidence Angle effect

For intermediate angles, the relative power density varies with the sine of the incident angle. The angle, sin(θ), is the angle between the Sun's rays the normal (or perpendicular) and the absorbing surface.  The Sine function you recall from high school trigonometry is 1 at 90 degrees and 0 at 0 degrees.  So, incidence angle of sunlight's arrow pointing straight down on the surface gives us max energy and any angle less than 90 degrees incidence gives us less than max energy.

The Incidence Angle equation in vCalc will provide the fraction of energy from the incidence angle.

The irradiance absorbed by the surface can be found by multiplying the total irradiance `I_T` by sin (θ).

`I_A = I_T sin(theta)`

                         Where
                                   `I_A`:  Irradiance absorbed by the surface
                                   `I_T` : Total irradiance
                                   `theta`:  Incident angle

Therefore under peak sun conditions (1,000 `"Watts"/"meter"^2`) if the angle of the sun's rays strike a surface 15° off from perpendicular, the irradiance absorbed the surface would be:

`I_A` = 1,000 `W/m^2` x sin(15°) = (1,000)(~.259) ≈ 259 `W/m^2`

Ultimately, this makes sense because the incident angle is 0° if the sunlight is directly normal to the absorbing surface and cos(0°) = 1, meaning that 100% of the available irradiance is absorbed by the surface. Similarly, when the surface is parallel to the Sun's rays, the incident angle is 90°, and because cos(90°) = 0, the surface absorbs no irradiance. In the above example, cos(15°) = .966, and so the surface is absorbing 96.6% of the available solar power. 

In designing photovoltaic (PV) systems, this question of how much available irradiance is absorbed by the photovoltaic modules is very important, since the amount of energy the system is able to produce is directly proportional to the amount of energy it absorbs from the Sun. Some systems are therefore designed with trackers on them, which cause the photovoltaic modules to follow the Sun's movement across the sky, maximizing the amount of time that the PV modules are directly normal to the sunlight. For fixed tilt systems, however, this is not possible, and so the system must be designed using the tilt angle and orientation that will best fits the needs of the system's owner. Most often, this means installing the system at the angle that will absorb the most irradiance over the course of the year, but in some cases there may be times when there is a critical need for energy and so the system can be designed to produce more electricity when it's most needed.