CHM1 11 Boiling Point Elevation and Freezing Point Depression Co

Boiling Point Elevation and Freezing Point Depression

The freezing point and boiling point of a pure solvent can be changed when added to a solution. When this occurs, the freezing point of the pure solvent may become lower, and the boiling point may become higher. The extent to which these changes occur can be found using the formulas:

`DeltaT_f = -K_f * m`

`DeltaT_f = K_b * m`

where m is the solute molality, and the K values are proportionality constants.

If solving for the proportionality constant is not the ultimate goal of the problem, these values will most likely be given. Some common values for `K_f` and `K_b`, respectively, are:

Solvent	`K_f`	`K_b`
Water	1.86	.512
Acetic Acid	3.90	3.07
Benzene	5.12	2.53
Phenol	7.27	3.56

Molality is defined as the number of moles of solute per kilogram solvent. Be careful not to use the mass of the entire solution. Often, the problem will give you the change in temperature and the proportionality constant, and you must find the molality first in order to get your final answer.

The solute, in order for it to exert any change on colligative properties, must fulfill two conditions. First, it must not contribute in the vapor pressure of the solution and second, it must remain suspended in the solution even during phase changes. Because the solvent is no longer pure with the addition of solutes, we can say that the chemical potential of the solvent is lower. Chemical potential is the molar Gibb's energy that one mole of solvent is able to contribute to a mixture. The higher the chemical potential of a solvent is, the more it is able to drive the reaction forward. Consequently, solvents with higher chemical potentials will also have higher vapor pressures.

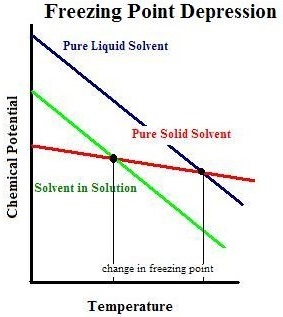
Boiling point is reached when the chemical potential of the pure solvent, a liquid, reaches that of the chemical potential of pure vapor. Because of the decrease of the chemical potential of mixed solvents and solutes, we observe this intersection at higher temperatures. In other words, the boiling point of the impure solvent will be at a higher temperature than that of the pure liquid solvent. Thus, boiling point elevation occurs. The increase in temperature is quantified using `DeltaT_b= K_bm` where `K_b` is known as the ebullioscopic constant and m is the molality of the solute.

Freezing point is reached when the chemical potential of the pure liquid solvent reaches that of the pure solid solvent. Again, since we are dealing with mixtures with decreased chemical potential, we expect the freezing point to change. Unlike the boiling point, the chemical potential of the impure solvent requires a colder temperature for it to reach the chemical potential of the solid pure solvent. Therefore, we observe a freezing point depression. We measure the change in the freezing point temperature using `DeltaT_f = K_fm` where K_f is known as the cryoscopic constant and m is again the molality of the solute.

Example 9

2.00 g of some unknown compound reduces the freezing point of 75.00 g of benzene from 5.53 to 4.90 °C. What is the unknown compound's molecular mass?

Solution:

First we must compute the molality of the benzene solution, which will allow us to find the number of moles of solute dissolved.

`m=T_f/-K_f`

`=((4.90-5.53)^@C)/(-5.12^@C"/"m)`

`=.0123m`

`"Amount Solute" = 0.07500 "kg benzene " X ((0.123m)/(1 "kg benzene "))`

`= 0.00923 "m solute"`

We can now find the molecular weight of the unknown compound:

`"Molecular Weight" = (2.00 "g unknown")/(0.00923 mol)`

`=216.80 g"/"mol`

The freezing point depression is especially vital to aquatic life. Since saltwater will freeze at colder temperatures, organisms can survive in these bodies of water.

Subpages (1): Example 9