Tags | |
UUID | 19b33e09-f145-11e9-8682-bc764e2038f2 |
Internal Energy
From UCDavis Chemwiki link 1 and link 2
Remember from a previous discussion:
The 1st Law of Thermodynamics
The First Law of Thermodynamics states that energy can be converted from one form to another with the interaction of heat, work and internal energy, but it cannot be created nor destroyed, under any circumstances. The equation that supports the First Law of Thermodynamics mathematically is:
ΔU=q+w
Here ΔU is the total change in internal energy of a system, q is the heat exchanged between a system and its surroundings, and w is the work done by or on the system. Work is also equal to the negative external pressure on the system multiplied by the change in volume:
w=-pΔV
where P is the external pressure on the system, and ΔV is the change in volume.
The internal energy of a system would decrease if the system gives off heat or does work. Therefore, internal energy of a system increases when the heat increases (this would be done by adding heat into a system). The internal energy would also increase if work were done onto a system. Any work or heat that goes into or out of a system changes the internal energy. However, since energy is never created nor destroyed (thus, the first law of thermodynamics), the change in internal energy always equals zero. If energy is lost by the system, then it is absorbed by the surroundings. If energy is absorbed into a system, then that energy was released by the surroundings:
ΔUsystem=-ΔUsurroundings
where ΔUsystem is the total internal energy in a system, and ΔUsurroundings is the total energy of the surroundings.
Table 1
| Process | Sign of heat (q) | Sign of Work (w) |
|---|---|---|
| Work done by the system | N/A | - |
| Work done onto the system | N/A | + |
| Heat released from the system- exothermic (absorbed by surroundings) | - | N/A |
Table 2
| The Process | Internal Emergy Change | Heat transfer of thermal energy (q) | Work w=PΔV |
Example |
|---|---|---|---|---|
| q=0 Adiabatic | + | 0 | + | Isolated system in which heat does not enter or leave similar to styrofoam |
| DeltaV=0 Constant Volume | + | + | 0 | A hard, pressure isolated system like a bomb calorimeter |
| Constant Pressure | + or - | enthalpy (ΔH) | -PΔV | Most processes occur are constant external pressure |
| DeltaT=0 Isothermal | 0 | + | - | There is no change in temperature like in a temperature bath |
Measurement of Internal Energy
Equation (1) tells us how to detect and measure changes in the internal energy of a system. If we carry out any process in a closed container the volume remains constant), the quantity of heat absorbed by the system equals the increase in internal energy.
qv (1)
A convenient device for making such measurements is a bomb calorimeter (Fig. 6), which contains a steel-walled vessel (bomb) with a screw-on gas-tight lid. In the bomb can be placed a weighed sample of a combustible substance together with O_2 (g) at about 3 MPa (30 atm) pressure. When the substance is ignited by momentarily passing electrical current through a heating wire, the heat energy released by its combustion raises the temperature of water surrounding the bomb. Measurement of the change in temperature of the water permits calculation of q_v (and thus DeltaU), provided the heat capacity of the calorimeter is known.
The heat capacity can be determined as in Example 1 from Heat Capacities or by igniting a substance for which DeltaU is already known.
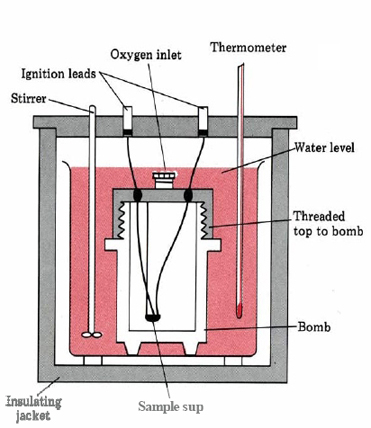
Figure 6 A schematic of a bomb calorimeter.
EXAMPLE 11 When 0.7943g of glucose, C_6 H_(12) O_6, is ignited in a bomb calorimeter, the temperature rise is found to be 1.841 K. The heat capacity of the calorimeter is 6.746 kJ K^(-1). Find DeltaU_m for the reaction
C_6 H_(12) O_6(s) + 6 O_2(g) -> 6CO_2 (g) + 6H_2 O(l)
under the prevailing conditions.
Solution:
The heat energy absorbed by the calorimeter in increasing its temperature by 1.841 K is given by
q = CDeltaT = 6.745kJ K^(-1) & 1.841K = 12.42kJ
Since this heat energy was released by the reaction system, we must regard it as negative. Accordingly,
q_v = -12.42kJ = DeltaU
We need now only to calculate the change in internal energy per mole, that is, DeltaU_m. Now
n_"glucose" = 0.7953g * (1mol)/(180.16g) = 4.409 * 10^(-3) mol
Thus
DeltaU_m = (-12.42kJ)/(4.409) * 10^(-3)mol = -2817kJ mol^(-1)

Subpages (1): Example 11
This Collection is empty
- Comments
- Attachments
- Stats
No comments |
