THIS EQUATION

This equation computes the force of friction (`F_f`)on an object which is stationary on an inclined plane.

APPLICATIONS

This equation defines the minimal force of friction required to keep the object in a static location on an inclined plane.  If the angle, (`theta`) of the plane is increased, the object will remain stationary on the plane only if the coefficient of static friction is great enough to provide a force of friction to offset the increased force of the parallel component of the gravitational force (`F_"g ||"`) on the object.

INPUTS

The inputs to this equation are:

• m - the mass of the car
• `phi` - the angle of the incline
• `mu` - the coefficient of friction characterizing the two surfaces interaction.

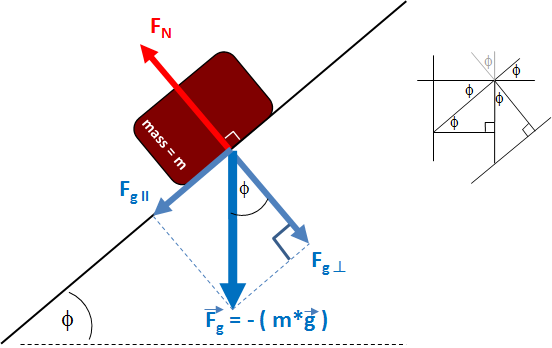
Notes

In the illustration, we see and object sitting on an inclined plane.  We assume the object is not moving on the plane.

We can see that the magnitude of the force parallel to the plane which is due to gravity (F_{g ||}) can be computed as:

`vecF_"g ||"   =   vecF_g) * sin(theta)`

So, the force of friction F_f in this example is exactly equal to and in the opposite direction of the force of gravity pulling the object down the incline plane.

`vecF_f    = -vecF_g * sin(theta)`

`|vecF_f|    = m* g * sin(theta)`