Processing...
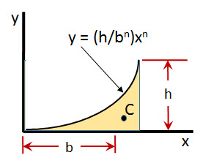
`"Area Moment of Inertia (I)" = I_x [ "n" , "b" , "h" ], I_y [ "n" , "b" , "h" ]`
Enter a value for all fields
This equation computes the `I_x` and `I_y` components of the Area Moment of Inertia for an nth degree parabola, concave up, where the equation for the parabola is y = `(h/b^(n)) x^(n)`. This assumes the parabola is defined in the x/y plane.
The Area Moment of Inertia (I), also called the second moment of area, polar moment of inertia or second area moment, represents how area is distributed around the center of mass. The Area Moment of Inertia has units of length to the fourth power.
Reference
Fundamentals of Engineering. 8th edition, 2nd Revision. National Council of Examiners for Engineering and Surveying (NCEES) - 2001. ISBN 978-1-932613-59-9. pg53