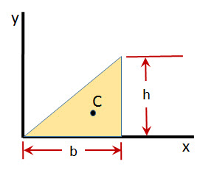
The Moment of Inertia of Right Triangle calculator computes the x and y components of the moment of inertia based on the base and height of the triangle.

INSTRUCTIONS: Choose units and enter the following:

• (b) Base of the triangle
• (h) Height of the triangle

Moment of Inertia (MoI): The calculator returns the MoI components in meters to the fourth (m⁴).

The Math / Science

The Area Moment of Inertia equation,  I = (b•h³)/12 , (b³•h)/4 , computes the Area Moment of Inertia for a right triangle with right angle on right of the base.   Right Triangle The output of this equation is the I_x and I_y components of the area moment of inertia when the triangle is defined to be in the x/y plane

The Area Moment of Inertia (I), also called the second moment of area, polar moment of inertia or second area moment, represents how area is distributed around the center of mass. The Area Moment of Inertia has units of length to the fourth power.

The Math

The formula for the moment of inertia is as follows:

            `I = ((b*h^3)/12)"," ((b^3*h)/4)`

Reference

Fundamentals of Engineering. 8th edition, 2nd Revision.  National Council of Examiners for Engineering and Surveying (NCEES) - 2001. ISBN 978-1-932613-59-9.  pg51