The Rotational Acceleration of a Physical Pendulum calculator approximates the rotational acceleration of a physical pendulum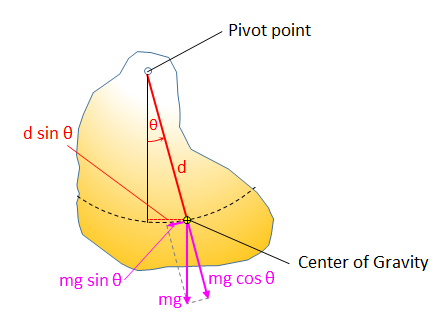 based on the mass (m), acceleration due to gravity (g), distance to the center of gravity (d), impulse (I) and the angle (Θ).

INSTRUCTIONS: Choose the preferred units and enter the following:

• (m)  Mass
• (d)  Distance to Center of Gravity
• (Θ) Angle Displacement
• (I) Moment of Inertia

Rotational Acceleration: The calculator returns the acceleration in radians per second squared (rad/s²).  However this can be automatically converted to compatible units via the pull-down menu.

The Math / Science

The Rotational Acceleration of a Physical Pendulum equation calculates the rotational acceleration of the physical pendulum given that θ is small. This is because sinθ is approximately θ. So this equation will give the approximate rotational acceleration given that the angle is small.

The Pendulum Calculator includes the basic physics formulas and constants for the properties of a pendulum.  These include the following:

• Pendulum Frequency: Computes the frequency (ƒ) of a simple pendulum based on the length (L) of the pendulum.
• Period of a Pendulum: Computes the period (T) of a simple pendulum based on the length (L) of the pendulum arm and the acceleration due to gravity (g).
• Pendulum Length: Computes the length (L) of a simple pendulum based on the period (T) of the pendulum arm and the acceleration due to gravity (g).
• Pendulum Angular Frequency: Computes the angular frequency of a simple pendulum with a small amplitude.
• Angular Frequency of a Physical Pendulum: Computes the approximate value of the angular frequency given that the amplitude of the pendulum is small based on the mass, distance from pivot point to center of mass and the moment of inertia.
• Restoring Torque to a Pendulum: Computes the restoring torque (τz) on a physical pendulum based on the mass (m), acceleration due to gravity (g), distance to the center of gravity (d) and the displacement angle (θ).
• Restoring Force on a Pendulum: Approximates the restoring force on a pendulum based on the mass, length of pendulum and length of arc. 
• Rotational Acceleration of a Physical Pendulum: Approximates the rotational acceleration of a physical pendulum based on the mass (m), acceleration due to gravity (g), distance to the center of gravity (d), impulse (I) and the angle (Θ)
• (g) acceleration due to gravity 

References

Young, Hugh and Freeman, Roger.  University Physics With Modern Physics.  Addison-Wesley, 2008. 12th Edition, (ISBN-13: 978-0321500625 ISBN-10: 0321500628 ) Pg 438, eq 13.37