A vector is a mathematical concept of an object that has direction and length.  A line alone is not a vector but a line with orientation spanning the distance between two arbitrary points in space is a vector.  This equation computes the component of a vector that is the vector's projection on the y-axis of Cartesian coordinates.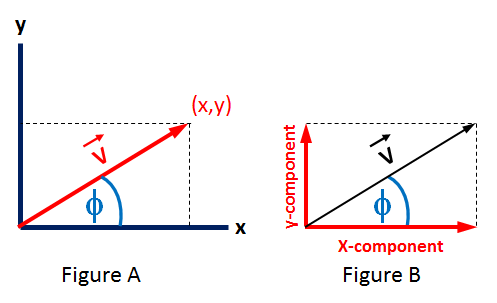

Description

Figure A shows a vector, `bar V` (in red) represented in Cartesian coordinates.  A vector can point in any direction, so there is no significance to the fact that `bar V` in Figure A is pointing to a point in the +x/+y quadrant of the Cartesian coordinates. 

The direction and length of `bar V` define it as a vector and the vector can be displaced to any point in space and still be vector `bar V`. The beginning of the vector does not have to be located at the intersection of the x and y coordinates. We show vector `bar V`, with it's beginning point at the origin to simplify the idea that the y-component is the projection of the vector onto the y-axis. The angle, `phi`, between the x-axis and the vector, `bar V`, is used in this equation to compute the y-component of the vector, the projection of the vector, `bar V` onto the y-axis.

Figure B shows the Cartesian x and y components of the vector `bar V`.  Figure B shows the vector `bar V` displaced from the vector shown in Figure A but the two vectors could be considered equivalent because they have the same length and they both point in the same direction.

See also

V2 - Vector (x-component)