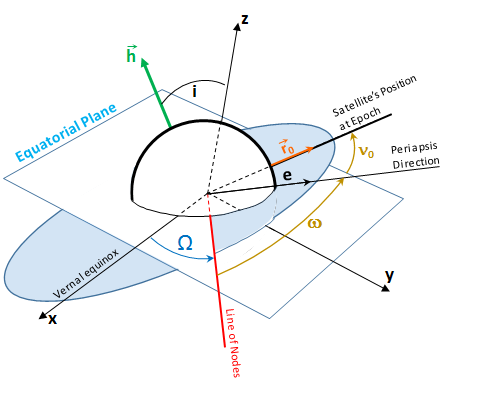
The Non-Spherical Earth perturbation equation for the rate of change of the argument of perigee, `dotomega`, of an orbit where the rate of change (`dotomega_"J2"`) in deg/day results from the `J_2` geopotential coefficients derived from the geopotential function of the Earth.  The inputs to this equation are:

• the mean motion of the orbit (n) in deg/day
• the Earth equatorial radius (`R_E`) in kilometers
• the orbit's semi-major axis (a) in kilometers
• the eccentricity of the orbit, (e)
• the orbit inclination (i)

Notes

The earth is not a sphere.  In fact, the Earth is neither a homogeneous mass nor a sphere.  Consequently, the several attributes of the Earth's shape and composition have noticeable affects on a satellite's orbit.  The bulge at the equator, the flattening at the poles, and the slight pear shape of the Earth are important contributors to the perturbation of an orbit due to a non-spherical Earth.