Radius of Displaced Circle

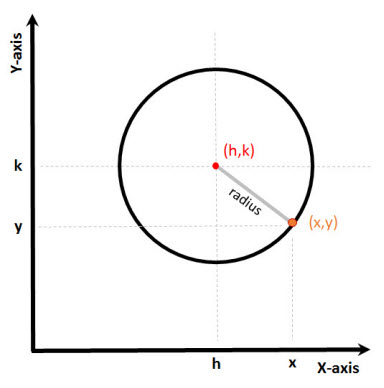
This equation computes the radius of a circle given that you know the circle's center  and a point anywhere on the circle. The circle's center can be placed anywhere in the X-Y Plane.

Our circle in this equation is centered at the point (h,k) and the point on the circle is (x,y)

Inputs:

• h - x-coordinate of the circle's center
• k - y-coordinate of the circle's center
• x - x-coordinate of a point on the circle
• y - y-coordinate of a point on the circle

Note all coordinates ( h, k, x, y ) should be in the same length units.