vCalc's Principle Plane Stress (?1 = ?_max) equation computes the first principal stress in a plane stress situation.

Inputs

• `sigma_x` - the x-component of normal stress
• `sigma_y` - the y-component of normal stress

Description

The equations for principal stress in the two-dimensional stress state reduce to a maximum and minimum value, `sigma_1` and `sigma_2` respectively because the the third principal stress is zero by definition.
The three roots of the principal stresses of the two dimensional stress state are labeled by convention¹ 

• `sigma_1` - the algebraically largest
• `sigma_2` - the algebraically smallest
• `sigma_3` - the other principal stress that is zero in the plane stress case

In continuum mechanics, an object or material is under plane stress when the stress vector is zero across a specified surface.² In other words, if we define the coordinate system in Euclidean 3-space so that the stress on the object is purely in two of the three component directions, then the stress is acting as a plane stress. When plane stress occurs over an entire element of a structure, the stress state can be represented by a tensor of dimension 2 (representable as a 2 × 2 matrix rather than 3 × 3).  This plane stress is often the case for thin plates.   Plane strain, the result of plane stress, is noticable in thick objects.

Plane stress typically occurs in thin flat plates that are acted upon only by load forces that are parallel to the plate's surface. In certain situations, a gently curved thin plate may also be assumed to have plane stress for the purpose of stress analysis. This is the case, for example, of a thin-walled cylinder filled with a fluid under pressure. In such cases, stress components perpendicular to the plate are negligible compared to those parallel to it.³

In other situations, however, the bending stress of a thin plate cannot be neglected. One can still simplify the analysis by using a two-dimensional domain, but the plane stress tensor at each point must be complemented with bending terms.⁴

Derivation

The stress at some point in the material is a plane stress if one of the three principal stresses (the eigenvalues of the Cauchy stress tensor) is zero. That is, there is Cartesian coordinate system in which the stress tensor has the form⁵:

     `sigma = [[sigma_x,0,0],[0,sigma_y,0],[0,0,0]]`  

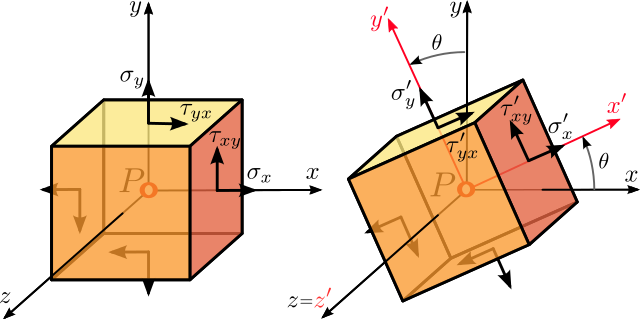
If we choose the x & y coordinates of our reference frame to be perpendicular to the direction of zero stress, then we can represent the stress tensor as:

     `sigma_"ij" = [[sigma_x,tau_"xy"],[tau_"yx",sigma_y]]`

This represents the stress tensor shown in the image.

See also

Principal Plane Stress (`sigma_2` = `sigma_"min"`)

1. ^ Fundamentals of Engineering. 8th edition, 2nd Revision.  National Council of Examiners for Engineering and Surveying (NCEES) - 2001. ISBN 978-1-932613-59-9.  pg 34
2. ^ http://en.wikipedia.org/wiki/Plane_stress
3. ^ http://en.wikipedia.org/wiki/Plane_stress
4. ^ http://en.wikipedia.org/wiki/Plane_stress
5. ^ http://en.wikipedia.org/wiki/Plane_stress