Kinetic Energy of a Rigid Body with Motion in the xy Plane

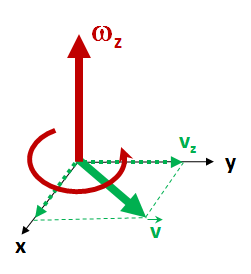
  This equation represents the energy possessed by a rigid body in motion traveling in the xy plane. In this formula, `KE` is a function of mass (`m`), velocity (`v`), mass moment of inertial ('Ic') and angular velocity (`omega`). This equation uses a component of the body's rotation that is normal to the xy plane and thus has component velocities in the x and y directions of the coordinate system.  The rotational element of the kinetic energy is a function of the angular velocity, `omega_z`, wich is perpendicular to the velocity components in the xy plane.

author:  Michael Bartmess

Notes

The kinetic energy of an object is the energy the object possesses due to its motion. It is defined as the energy acquired as a body accelerates from rest to a specified velocity. A body (a mass) maintains its kinetic energy until its velocity changes; for example, when a mass hits another immovable object and comes to a stop, its kinetic energy is transferred to another form of energy such as heat.

In classical mechanics, the kinetic energy of a non-rotating mass traveling at a speed v is `(1/2) *mv^2`. In relativistic mechanics, this model is only a good approximation when the velocity, v, is much less than the speed of light.