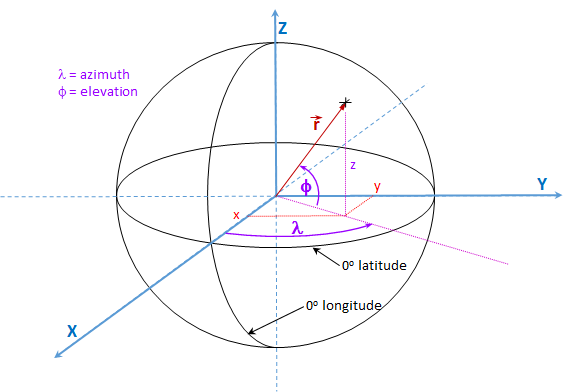
This equation computes the ECEF unit vector's y-coordinate of a point on the celestial sphere from input azimuth and elevation defined in the same Celestial sphere coordinate system.
Notes
The Celestial Sphere is defined by two poles. The equator is a great circle defined to be halfway between the two poles. The +x-axis points to the reference point on the equator's great circle, from which the longitude is measured counter clockwise about the North pole, The +z axis points to the positive North pole.
If the Celestial Sphere is imagined to be analogous to the Earth in this coordinate system geometry, Azimuth is equivalent to the longitude on the Earth's surface measured along the Earth's equator. A celestial sphere azimuth is measured counter clockwise from the reference point that is the intersection of the x-axis.
In this same analogy, the Celestial Sphere elevation angle is measured in arc length distance above or below the equator.
Note that the co-latitude and co-elevation are the arc lengths measured from the poles to some point.