The Central Angle of Horizon calculator computes the radial angle of the Earth at which an observer can see the horizon. In other words, this calculator reports the angle measured around a great circle of the Earth to a point on the horizon.
The Earth's shape is approximated as a sphere in this calculation.
USING THE CALCULATOR
h is the height of the viewing location that you enter into vCalc. If you are looking at the horizon from the top of a mountain, the height of the viewing location should be the height of the mountain plus the height of you eye or viewing instrument.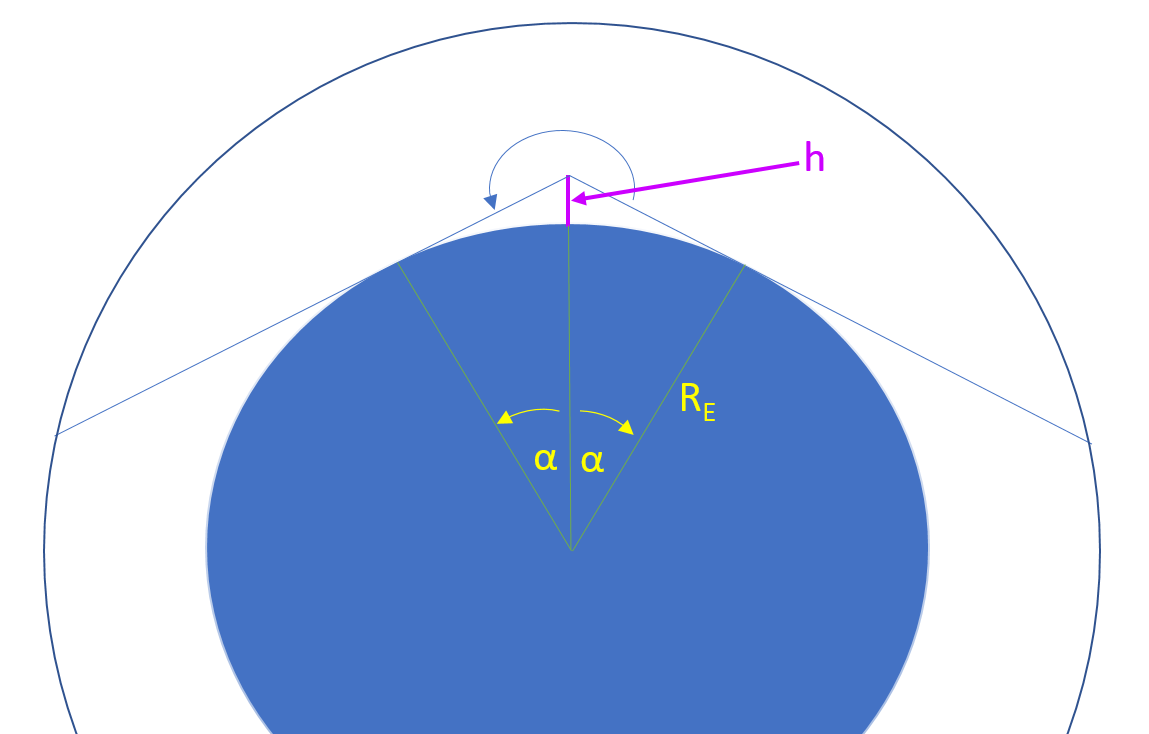
THE MATH
This equation uses the radius of the Earth (RE) and the altitude of the location from which the horizon is observed (h).
Since the site line is tangent to the circle, the triangle including angle α is a right triangle. The angle, α, can be computed with line through the tangent point having a length equal to the Earth's radius. The hypotenuse of the triangle is then the sum of the radius of the Earth and the altitude of the viewing location.
RE is the radius of the Earth, which is the vCalc constant: Earth - mean spherical radius (Km)
h is the height above the Earth's mean radius
cosine (α) = RERE+h→α = acos (RERE+h)
EXAMPLE
If we were to view the horizon from the top of a mountain that is 3 kilometers at its summit, this Central Angle of Horizon equation would tell us the central angle of the tangent point at the horizon is approximately 3.51591974 degrees from the viewing location.
SEE ALSO