Tags | |
UUID | 4ad5f2e5-b81f-11ec-be52-bc764e203090 |
Compound Interest calculator
Description
The combined daily interest rate is calculated using the simplified version of the compound interest formula. Multiply your main principal by one and the daily interest rate (such as decimal) increased by the number of days you invest. Subtract the principal from your total if you just want the interest rate.
With some types of investments you may find that your interest rate is accumulated daily, which means you earn interest on both the principal amount and interest accumulated on a daily basis. This often happens in day-to-day trading with bitcoin and other cryptocurrency trading platforms. Since interest is always compounded on a fixed basis, it could mean that the interest you earn is growing faster, as the interest rate per day is higher than the previous day.
Background
With it being a modified version of the Compound Interest calculator which the combined interest earned and the capital on the initial investment of a certain amount (P) by the fixed interest rate (r) over the period (t) and the number (n) of the combined events for each period. This formula is often used for bank savings accounts and other simple investments. Banks often offer interest-bearing savings accounts on a daily basis. In that case, a person may enter a total of savings (t) years and 365 (n) inclusive events each time for a number of days in a year. Combined descendants were once considered the principal offspring of the Roman Empire. Albert Einstein is reported to have said, "Consolidated offspring is the eighth wonder of the world. He who understands, receives it. Whoever does not pay, pays for it."
(P) Principal invested (e.g. 400,000 Ksh)
(r) Interest rate per period (e.g. 12% per year)
(t) Number of periods (e.g. 12 years)
(n) Number of payments per period (e.g. 12 payment in a year for "Compounded Monthly")

Figure 1
Benefits of compound interest became apparent as one could continually earn more over time.
To give a graphical example, the graph below shows the result of $1000 invested over 20 years at an interest rate of 10%. The principal figure is in green. The blue part of the graph shows the result of 10% interest without compounding. Finally, the purple part demonstrates the benefit of compound interest over those 20 years.
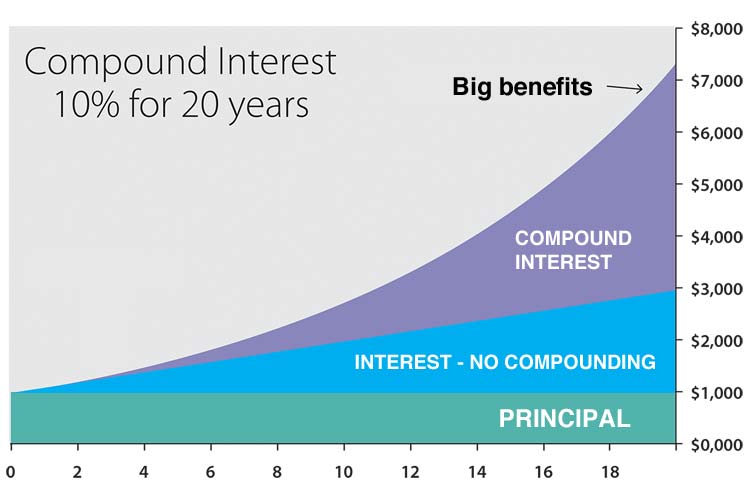
Figure 2
the compound interest formula began fairly short and expanded and evolved based upon peoples requests for adapted formulae and examples.
This later resulted in the creation of the formulas below
Formula for calculating interest rate (r)

Figure 4
Formula for calculating principal (P)

Figure 5
Purpose
The formula for daily compound interest with a daily interest rate that is fixed is:
A=P(1+r)t
Example
With an example of $1,000 at 0.4% daily for 365 days.
P = 1000
r = 0.4/100 = 0.004
t = 365
A = P(1+r)t
A = 1000(1+0.004)365
A = 1000 * 4.2934377972993
A = 4293.4377972993
- Comments
- Attachments
- Stats
No comments |
