Centroid - nth Degree Parabola (convex)

The Coordinates of the Centroid of an nth Degree Parabola calculator provides the x and y coordinate of the centroid of a parabolic area segment based on the exponent (n) and the base (b) and height (h) measurements.

INSTRUCTIONS: Choose units and enter the following: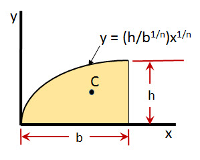

• (n) Exponent
• (b) Base
• (h) Height

Centroid Coordinates (C_(x,y)): The calculator returns the coordinated in centimeters.  However, these can be automatically converted to compatible units via the pull-down menu.

The Math / Science

The Coordinates of a Centroid of an nth Degree Parabola equation computes the x and y components of the Centroid for an nth degree parabola, convex up, where the equation for the parabola is y = `(h/b^(1/n)) x^(1/n)`

The formula for the centroid coordinates are:

C_y = `((n+1) * h) /( 2*(n+2) )`

C_x = `((n+1) * b) / (2*n+1)`

where:

• Cy = y coordinate of centroid
• Cx = x coordinate of centroid
• n = exponent of parabola equation
• b = length of the base
• h = length of the height

The calculator also returns the area (A) of the parabola section, where the formula is:

A = (n • b • h) / (n +1)

The Centroid (C) represents center of mass of the parabola. The Centroid has x & y units of length representing a coordinate.