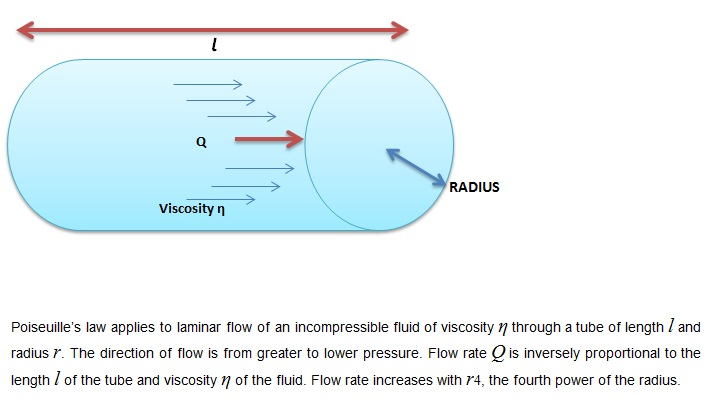
Laminar flow is characterized by the smooth flow of the fluid in layers that do not mix.For laminar flow, resistance is quite low. Therefore a relatively small driving pressure is needed to produce a certain flow rate. Laminar Resistance is also called Poiseuille’s law for resistance after the French scientist J. L. Poiseuille (1799–1869), who derived it in an attempt to understand the flow of blood, an often turbulent fluid. 

Poiseuille described that the resistance exerted by a tube to the flow of a substance,R = 8etal / πr4

Where: eta = viscosity of the substance

l = length of the tube

r = the radius of the tube

The most important variable here is the radius, which, due to its elevation to the fourth power, has an enormous impact on resistance. Thus, if the diameter of a tube is doubled, resistance will drop by a factor of sixteen.

Notes

Laminar Flow is streamlined such that the fluid at the center of the tube moves the fastest. In Latin, laminae means layers and laminar flow refers to circular layers of fluid movement with the fastest being in the center to the slowest at the walls of the tube. Therefore, laminar flow has a parabolic velocity profile. During laminar flow the relationship between driving pressure and flow is linear and  with an increase in driving pressure, flow will increase proportionally. Flow in small airways (diameter < 2mm) is laminar silent and slow.

Airway resistance caused by the forces of friction is inversely proportional to air flow. It is defined as the ratio of driving pressure to the rate of air flow. Resistance to flow in the airways depends on whether the flow is laminar or turbulent, on the dimensions of the airway, and on the viscosity of the gas.We learn that resistance is directly proportional to both fluid viscosity η and the length l of a tube. Both of these directly affect the amount of friction encountered—the greater either is, the greater the resistance and the smaller the flow. The radius r of a tube affects the resistance, the greater the radius, the greater the flow (all other factors remaining the same). But it is surprising that r is raised to the fourth power in Poiseuille’s law. This exponent means that any change in the radius of a tube has a very large effect on resistance. For example, doubling the radius of a tube decreases resistance by a factor of 24=16.