This equation computes the wind-corrected  flight azimuth that is required to follow the ground path to an aircraft's flight destination.

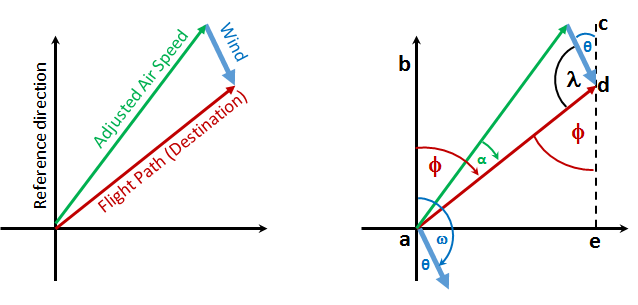
The diagram shows the Adjusted Air Speed vector that results from the vector subtraction of the wind vector from the destination flight path vector.

As inputs to this equation we have:

• `omega` - the azimuth angle of wind vector from the reference direction.
• `phi` -  the azimuth angle of the flight path from the reference direction
• `FP` - the flight path speed
• `W` - the wind speed

Notes

In the diagram we know the angle, `omega`, of the wind's direction and the angle, `phi`, of the planned flight path to the destination.  The planned flight vector is the maroon arrow of length FP in this example that is `phi` degrees clockwise from the reference direction.  In this example the reference direction is the line (a,b).  The line (a,b) could very well be the compass vector North, making the line (a,e) the east vector.  We also know the length of the wind vector, `W`.

We know that angle `theta` is `180^o` minus omega.  We draw the line (c, d, e) parallel to the reference direction, making angle ade the opposite interior angle to `phi`.

So, now that we know angles `phi` and `theta`, we can find angle `lambda`.

`lambda` = 180 - (`theta` + `phi`) = 180 - (180 - `omega`)  - `phi`

`lambda` = 180 - 180 + `omega` - `phi`

`lambda` =  `omega` - `phi`

Using the Cosine Rule, to find the Adjusted Air Speed (AAS) we have:

`"AAS"^2 = "FP"^2 + W^2 - 2 * FP * W * cos(lambda)`

`"AAS"^2 = "FP"^2 + W^2 - 2 * FP * W * cos(omega - phi)`

`"AAS" = sqrt( "FP"^2 + W^2 - 2 * FP * W * cos(omega - phi))`

Then using the Sine Rule:

sin (`alpha`) / W = sin (`lambda`) / AAS  `=>`

`alpha` = arcsine`( (W* sin (lambda)) / "AAS") ` = arcsine`( (W* sin (omega-phi)) / (sqrt("FP"^2 + W^2 - 2 * FP * W * cos(omega - phi))) )`