Ellipse Mean Radius Integrated

The Ellipse Mean Radius Integrated calculator computes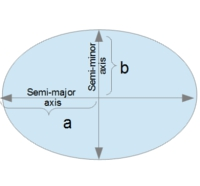            Ellipse an average radius (r_μ) of an ellipse based on the semi-major (a) and semi-minor (b) axes of the ellipse.

INSTRUCTIONS: Enter the following:

• (a)  Semi-Major axis Ellipse.
• (b)  Semi-Minor axis Ellipse.

Ellipse Mean Radius (r): The calculator returns the mean radius (r_μ) the same units as the axes. 

The Math / Science

In mathematics, an ellipse is a curve in a plane surrounding two focal points such that the sum of the distances to the two focal points is constant for every point on the curve. As such, it is a generalization of a circle, which is a special type of an ellipse having both focal points at the same location. The shape of an ellipse (how "elongated" it is) is represented by its eccentricity, which for an ellipse can be any number from 0 (the limiting case of a circle to arbitrarily close to but less than 1. 

This formula uses the average of 100 measurements of the radius

where:

• r_u is the mean radius of the ellipse
• a is the length of the semi-major axis.
• b is the length of the semi-minor axis.

Since the Earth is an oblate spheroid, closely approximated by an ellipsoid, the IUGG defines the Earth's mean radius using:

• a =  Equatorial radius (6,378.1370 km)
• b =  Polar radius (6,356.7523 km)

This computes and Earth mean radius of 6,371.009 kilometers (3,958.761 mi).

Related Ellipse calculators

• Area of an Ellipse: This computes the area of an ellipse based on the length of the axes. 
• Rumanujan's Circumference of an Ellipse 1:  This is the first of two of Rumanujan's approximations of the circumference (perimeter) of an ellipse based on the semi-major axis (a) and the semi-minor axis (b).
• Rumanujan's Circumference of an Ellipse 2: This is the second of Rumanujan approximations of the circumference (perimeter) of an ellipse based on the semi-major axis (a) and the semi-minor axis (b).
• Circumference of an Ellipse (other) This is another common estimation of the circumference (perimeter) of an ellipse based on the semi-major axis (a) and the semi-minor axis (b).Conic Sections
• Eccentricity of an Ellipse:  This computes the eccentricity of an ellipse which is based on the ratios of the semi-major axis (a) and the semi-minor axis (b).
• Mean Radius of an Ellipse:  This compute the mean radius of an ellipse.  This would define a circle with the same approximate area, based on the ellipse's semi-major axis (a) and the semi-minor axis (b).
• Linear Eccentricity of an Ellipse: This computes the linear eccentricity of an ellipse.

Reference

Description of an ellipse is from Wikipedia (en.wikipedia.org/wiki/Ellipse)