The Torque Required to Raise a Load with a Square Thread Power Screw calculator computes the torque (TR) required to raise a load using a Square Thread Power Screw assembly based on the following inputs:
Friction Coefficients (`mu, mu_c`)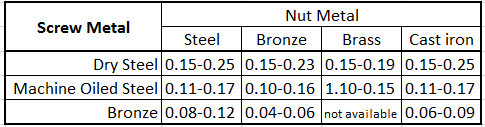
- (L) The length of the Lead.
- (F) The force of the Load.
- `mu` = coefficient of friction for thread
- `mu_c` = coefficient of friction for collar
- `d_m` = mean thread diameter
- `d_c` = mean collar diameter
The calculator returns the torque (TR) in Newtons per centimeter. However the user can automatically convert this to other torque units via the pull-down menu.
Common friction coefficients (μ,μc )based the thread and collar materials are provided in the table above.
The math
The formula used is as follow:
`T_R= F*d_m/2((L+pi*mu*d_m)/ (pi*d_m- mu*L)) + (F*mu_c*d_c)/2`
author: Carol
Notes
Square Thread Power Screws (Torque Required to Raise)
This equation accounts for the force required to overcome friction between the screw and the nut, in addition to the force required to raise the load. If the screw or the nut bears against a stationary surface while rotating, there will be an additional friction torque developed at that surface. For this reason, many jacks and similar devices incorporate friction-minimizing bearings at such points.
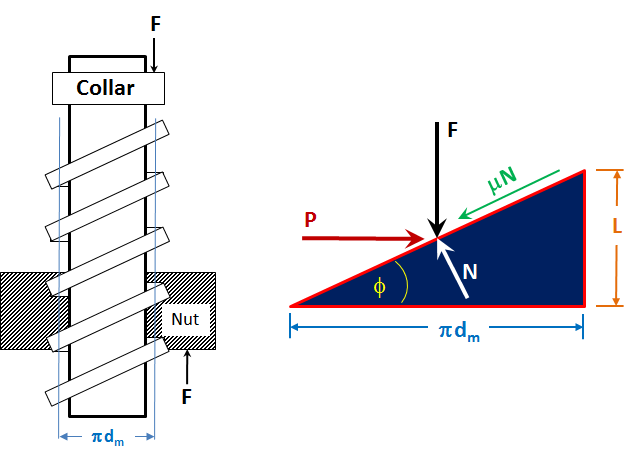
The coefficient of friction depends on the materials used and the lubrication between screw and nut. For well-lubricated steel screws acting in steel nuts `mu` = 0.15 would be conservative. The rotation of the screw tends to raise the load (move it up the incline), the friction force opposes the motion and acts down the plane.
Raising the load requires an axial force P as shown in the picture. N is the normal force and the force due to friction then acts to oppose the motion up the plane and is given by `mu * N`.
When the forces are in equilibrium, the equation F + `mu * N * sin(theta)` - `N * cos(theta)` = 0, which can be re-written to define the normal force, N, as a function of the the angle, `theta` (the angle of the contact surface to the plane perpendicular to the axis of the screw).
N = F(cos(`theta`) - `mu *sin(theta)`
Similarly, `P - mu * N * cos(theta) - N * sin(theta)` = 0, which gives P as a function of the angle `theta`:
P = `F(mu*cos(theta) + sin(theta) ) / (cos(theta) - mu* sin(theta))`
`T_R = F* d_m * (mu*cos(theta) + sin(theta) ) / (2* (cos(theta) - mu* sin(theta) )` and then we substitute `tan(theta) = L/`pi*d_m`
`T_R = (F*d_m/2) * (mu* pi * d_m + L) / (pi * d_m - mu *L)` -- the torque necessary to raise the load