Magnus Effect on a Cylinder

Last modified by

on

Sep 29, 2022, 12:51:44 AM

Created by

on

Jul 17, 2015, 11:35:18 PM

Lift = ρ \cdot V \cdot {(2 \cdot π \cdot r)}^{2} \cdot ω \cdot L

$"Lift" = rho * "V" * (2 * pi * "r" )^2 * omega * "L"$

(V) Velocity

$(V)"Velocity"$

(ρ) Density

$(rho)"Density"$

(r) Radius

$(r)"Radius"$

(ω) Rotational Rate

$(omega)"Rotational Rate"$

(L) Length

$(L)"Length"$

Related Calculators

Volume of a Cylinder
Mass of a Cylinder
Surface Area of a Cylinder and Flettner aeroplanes, where the rotating surface is a cylinder instead of a ball.¹

To understand the physics behind the Magnus effect we consider the conservation of momentum and the fact that the force on the body is approximately the equal and opposite force that the body imposes on the air flow around it, an expression of Newton's Third Law of motion. An upward lift force is created by a total summed deflection of the wake in the air flow downward.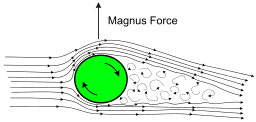 /attachments/7bf636d7-2cdc-11e5-a3bb-bc764e2038f2/256px-Sketch_of_Magnus_effect_with_streamlines_and_turbulent_wake.svg.png
Sketch of Magnus effect with streamlines and turbulent wake,
Wikipedia / Rdurkacz _{CC BY-SA 3.0}

For a rotating cylinder, the lift force is due to the angular deflection of the turbulent "wake" behind the moving cylinder. This can be visualized as the wake behind a moving cylinder (which creates aerodynamic drag) experiencing a noticeable angular deflection in the direction of the rotation of the cylinder. This is shown in the picture to the right. Notice that the cross-sectional view of the fluid flow in this diagram traces a contours very similar to the airflow over a airplane wing.

In the case of a spinning baseball, lift is produced on a back-spinning ball when the turbulent wake trailing the ball is deflected downwards. The rotation of the ball causes the boundary layer motion to be more turbulent beneath the ball where the rotation of the ball's surface is forward.

DERIVATION
On a cylinder, the force due to rotation can be defined in terms of the vortex produced by rotation. This force is also known as Kutta-Joukowski lift. The lift force $F$ $F$ per unit length on a cylinder is $\frac{F}{L}$ $F/L$ and $F$ $F$ is the product of the velocity, $v$ $v$ (in metres per second), the density of the fluid, $?$ $?$ (in kg per cubic meters), and the strength of the vortex that is established by the rotation, $G$ $G$ .

$\frac{F}{L} = ρ \cdot v \cdot G$ $F/L = rho * v * G$

`G = ( (2*Pi * r)^{2 ) * s $, w h e r e$ $, where$ s $i s t h e r o t a t i o n o f t h e c y l \in d e r \in r o t a t i o n s p e r \sec o n d and$ $is the rotation of the cylinder in rotations per second and$ r` is the radius of the cylinder.}

Magnus Effect on a Cylinder

Related Calculators

See Also

Datasets

Equations and Data Items

Calculators

Equations and Data Items

Collections