Non-directional Power Density

This Non-directional Power Density equation computes the power experienced at an object at some distance from a source of electromagnetic waves.  This equation is the basis of the radar range equation.

This is an ideal model approximation based on electromagnetic waves propagating without dispersion.

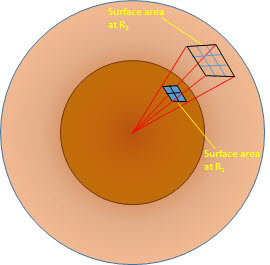
The diagram shows two concentric spheres representing the outward expansion of radiation from a point source.  The cells in the two marked surface areas depicted in the diagram are n concentric surfaces at radius R1 and radius R2.  Each cell of these two marked areas is the same dimension, showing that the power radiated outward is spread over a larger area (nine cells) at radius R₂ than at radius R₁ (4 cells).  

Radiating energy emitted by an isotropic radiator will propagate uniformly in all directions. Surfaces with the same power density therefore form spheres centered around the radiating source and the surface area of any one of these spheres is `4 π R^2`. The same energy spreads out and reaches the spherical surface at radius, R₁ as does reach the spherical surface R₂. 

All this means is that the power density on any surface is inversely proportional to the radius squared.  The power density decreases as the surface area it reaches increases by a square of the radius.