Multiplication of a 3x3 Matrix and a 3x1 Matrix

The Multiplication of a 3x3 matrix (A) and 3x1 matrix (B) calculator computes the resulting 1x3 matrix (C) of this matrix operation. 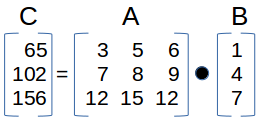  Matrix Multiplications 

INSTRUCTIONS  Enter the following:  

•  (A) 3x3 matrix 
•  (B) 3x1 matrix

1x3 MATRIX MULTIPLICATION (C): This calculator computes the resulting 3x1 matrix C.  Note: the 3x1 is returned as a single row with commas separating the values (e.g. [ [65],[102],[156] ] in the example above). 

The Math / Science

Matrices consist of rows and columns, where given a matrix `A`, the position in `A` in vCalc is denoted `A_(ij)` where the `1^(st)` subscript indicates the row of the matrix and the `2^(nd)` subscript indicates the column of the matrix. We refer to `A_(ij)` as the `(i, j)"th"` element of the matrix `A`. An arbitrary matrix has its size denoted as `mtimesn`, where `m` refers to the number of rows in a given matrix and `n` refers to the number of columns in a given matrix. 

If `m=n` then the matrix is referred to as a square matrix. The elements of the matrix `A_(11), A_(22), ..., A_(text(nn))` is commonly referred to as the main diagonal of the square matrix. 

Scalar Multiplication

Let `A` be a matrix and `c` be an arbitrary scalar number; scalar multiplication of `A` by `c` is "the matrix obtained by multiplying every element of `A` by `c`. The matrix `cA` will be the same size as `A`" (Williams, 37). 

Matrix Multiplication

Multiplying matrices is done by multiplying the rows of the first matrix with the columns of the second matrix in a systematic manner. In order for us to be able to multiply two matrices together, the number of columns in `A` has to be equal to the number of rows in `B`. Otherwise, the product `AB` of two matrices does not exist.
The matrix multiplication rule is as follows:
"Interpret the first matrix of a product in terms of its rows and the second in terms of its columns. Multiply rows times columns by multiplying corresponding elements and adding" (Williams, 37). 

Examples

Consider the following matrices `A` and `B`:

     `A= [(3, 1, 2), (4, 1, 5)], B=[(7, 2), (6, 3), (5, 1)]`

Since `A` has three columns and `B` has three rows, we know we can multiply these matrices to get a new matrix. We use the `AB` multiplication rule to get

     `AB= [( (3*7)+(1*6)+(2*5) , (3*2)+(1*3)+(2*1)), ((4*7)+(1*6)+(5*5) , (4*2)+(1*3)+(5*1))]`
     `AB=[(37, 11), (59, 25)]`

Now let's note an example from Williams on page 39: 

"Consider the following matrices `A` and `B`:

     `A= [(3, 1, 2), (4, 1, 5)],  B=[(7, 2), (6, 3)]`

Let us attempt to compute `AB` using the matrix multiplication rule.  We get

     `AB= [(3, 1, 2), (4, 1, 5)]*[(7, 2), (6, 3)]= [([(3, 1, 2)]*[(7), (6)],[(3, 1, 2)]*[(2), (3)]),( [(4, 1, 5)]*[(7), (6)], [(4, 1, 5)]*[(2), (3)]) ]`

If we try to compute `[(3, 1, 2)]*[(7), (6)]`, the elements do not match, and the product does not exist. The same shortcoming applies to all the other elements of `AB`. We say that the product `AB` does not exist."

The following properties of matrix multiplication are important to know: 1) Matrix Multiplication is not commutative 2) If `A` is an `m times r` matrix and `B` is an `r times n` matrix, then `AB` will be an `mtimesn` matrix. 

Matrix Calculators

• Determinant of 3-by-3 Matrix
• Characteristic Polynomial of a 3x3 matrix
• Inverse of a 3x3 Matrix
• Transpose of a 3x3 Matrix
• Trace of a 3x3 Matrix
• Mirror of a 3x3 Matrix
• 3x3 Matrix Characteristics (Trace, Determinant, Inverse, Characteristic Polynomial)
• Product of a 3x3 matrix and a Scalar
• Product of a 3x3 matrix and a 3x1 matrix
• Product of two 3x3 matrices
• Solving 3 Equations with 3 Unknowns
• Cramer's Rule (three equations, solved for x, y and z)
• Cramer's Rule Calculator

Sources

Williams, Gareth. Linear Algebra With Applications. Boston: Jones and Bartlett, 2011. Print.