Conversion from Cartesian Coordinates to Cylindrical Coordinates

Quoting Bray, "When we talk about points in `RR^2` or `RR^3,` we refer to a specific point with a set of coordinates. In `RR^2` we need two coordinates, and in `RR^3` we need three coordinates. These coordinates are defined by a set of conventions, defining a 'coordinate system' " (43).

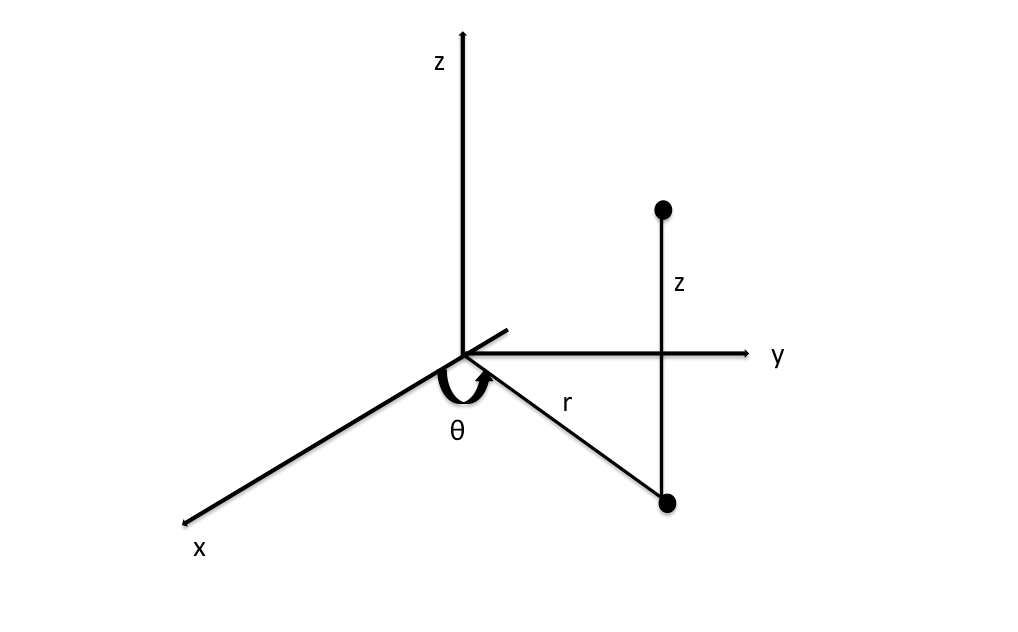
The coordinate system that people are usually familiar with is the Cartesian Coordinate System. The Cartesian Coordinate System in `RR^3` pinpoints the location of a point by using the `x`, `y`, and `z` axes and providing the numerical value on each axis of where a particular point can be found. The reason why the Cartesian Coordinate System is used more frequently than other coordinate systems is because every point has a unique set of coordinates, and the coordinates do not overlap or repeat.  There are times when other conventions may be more useful, which is why one might wish to convert from Cartesian coordinates to Cylindrical coordinates. 

Given a point `(x, y, z)` in `RR^3,`cylindrical coordinates are of the form `(r, theta, z)`,  where:

• The coordinate `r` is defined as `r = sqrt(x^2 + y^2)` 
• The coordinate `theta` is defined as `theta = tan^(-1) (y/x)`
• The coordinate `z` is defined as `z=z`, and does not change from the Cartesian "`z`" coordinate

In the image located above, the coordinate "`r`" is the "polar `r`-coordinate of the projection of (the point) into the `x-y` plane" (Bray, 45). The coordinate "`theta`" is the " polar `theta`-coordinate of the projection of (the point) into the `xy`-plane" (Bray, 45). The coordinate `z` is the cartesian "`z`" coordinate. 

Cylindrical Coordinates are similar to Polar Coordinates in `RR^2,` as we mentioned above that `r` and `theta` are defined the same way for Polar coordinates. For this reason, you may wish to check our conversion equation from cartesian to polar coordinates. 

Sources

Bray, Clark. Multivariable Calculus. Middletown, DE: n.p., 2015. Print.