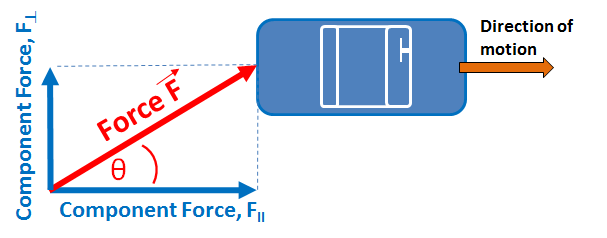
This equation computes the component force in the direction of transmission of the force. In the picture the magnitude of the force `bar F` is incident on an object (a car in out example) and the component of the force that is projected parallel to the car's direction is `bar F_"||"`.  Thus the portion of the force, `bar F`, that will cause the car to move forward is the parallel component of the force.  In this example, the perpendicular component of the force is transmitted into the frame of the vehicle and probably would not result in motion of the car.

Notes

This example of a force being applied to a vehicle at an angle to the direction of the car's motion is a simple problem of defining the components of the force,`bar F`, applied.  In this case you can determine the component of the force parallel to the car's direction of motion and perpendicular to the car's direction of motion; i.e., in the direction of the tires or 90 degrees to the tires' direction. 

Let's assume for a second the force, `bar F`, is from another vehicle hitting the car in the picture.  If that other vehicle hit the car at an angle, `theta`, where `theta is greater than zero,` this equation tells us that not all of the force of the collision would be transmitted into the motion of the vehicle in the picture.  A portion of the force, `bar F`, would be transmitted in the direction perpendicular to the car's direction of travel.  This perpendicular component could tip the car, depending on the magnitude of the impact force, but would likely be absorbed by deformation of the car and/or the suspension of the car.  On the other hand the parallel component of force would act to move the car in its direction of travel.

Note that if the angle`theta` were zero, then the force, `bar F`, would be wholly parallel to the car's direction of travel, and thus ALL of the force would be transmitted in the direction of the car's direction of motion. The equation demonstrates that fact, since the cosine of zero degrees is 1.

If on the other hand the angle `theta` were 90 degrees, then all of the force, `bar F`, would be transmitted perpendicular to the vehicle in the example.  None of the force would be applied to the car in it's direction of motion and this is also demonstrated by the equation, since cosine of 90 degrees is zero.