Circular Permutations

This equation computes the number of ways that you can arrange n unique objects around a circle. 

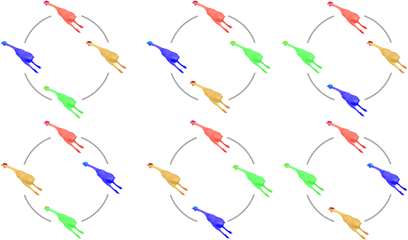
As you can see illustrated below, a set of four brightly colored dead chickens can be arranged circularly in six different circular permutations.

The number of circular permutations of four unique elements: `P_4` = (4 - 1) ! = `3*2*1` = 6.  This means the probability of getting one specific circular permutation from four unique elements is 1 in 6.

This is the special case of computing the number of r-permutations of a set of n elements, where r =  n.

Since the number of linear permutations is computed as: `P(n,r) = (n!) / ((n-r)!)`, the number of circular permutations is `(P(n,r)) / r`

This in turn gives us the number of circular permutations as `(n!) / r*(n-r)! = (n!) /r *0! = (n-1)!`

Circular Permutations of Colored Dead Chickens

Here we illustrate the six circular permutation of a set of four unique items -- in this case four differently colored dead chickens.

-- remembering Miss Starrett's class

APPLICATION

A circular permutations can be seen in the relationship between proteins, where the order of peptide sequences within a set of proteins can be arranged in different permutations.  This permutation calculation can then compute the number of possible proteins that can be constructed of the set of n peptide sequences.

Engineering strategies to explore protein sequences have been used to enhance the function of old yellow enzyme (OYE), which can be used as a bio-catalyst for stereo-selective trans-hydrogenation of activated alkenes.  See abstract: http://pubs.acs.org/doi/abs/10.1021/ja4074886.

Circular permutations come into play in many kinds of combinatorics problems.