Your Search

OK, so you've entered the dating scene and are wondering how long it's going to take to find your perfect match. 

Here's some food for thought and maybe some ideas for what to consider in your search.  It always helps to be a little introspective and using this equation as a thought problem can uncover veiled ideas of what is most important to you.

This equation computes the number of people who might be a perfect match for you based on a number of lifestyle and personality factors which characterize your perfect match. 

This equation assumes these factors are applied to the set of people comprised by the population in which you are willing to search for a partner.  It obviously should show that the wider the population you consider, the greater the chances of finding your perfect life partner. But that's just the first question that should come to mind when considering what is most important to you. 

If you look in only a close neighborhood, you chances may be very small by definition.  So, it is worth considering what are you really trying to accomplish in your search -- find a relationship that will last, or just find someone easy to access.

The thought process you put into this equation also shows that placing importance on factors which are really not important to you can seriously hurt your chances of finding your perfect match.  This isn't to say you should settle but instead that you should look at the factors that influence your decisions and see if there are not some places you can work on imbuing your own personality with improvements that will ultimately make you happier.

Input Compatibility Factors

Each of the fractional factors can be set to other than the default but the value should be greater than zero (although can be really tiny if you think that factor is unlikely).

Each factor should be less than or equal to one.  Setting a value to one means that factor will always be true.  For example setting the Fraction Found Attractive to one means you believe all people you meet are attractive, which is unrealistic and in the algorithmic sense will remove attractiveness from consideration.

The input factors considered are:

• Target Population - the size of the population you are willing to search
• Fraction Targeted Gender - % population in preferred gender
• Fraction Single -% population that are single
• Fraction May Encounter - % population you may encounter
• Fraction in Age Range - % population in your preferred age range
• Fraction Speak Your Language - % population speaking your language
• Fraction Trustworthy - % of population who would be considered trustworthy in a relationship
• Fraction Found Attractive -  %population you consider attractive
• Fraction Find You Attractive - % population which consider you attractive
• Fraction Intelligence - % population matching intelligence expectations
• Fraction Political - % population matching your political tastes
• Fraction Religious - % population same religious beliefs
• Fraction Funny - % population you would find funny
• Fraction Cuddle - % population cuddle same
• Fraction Sex - % population who like sex as much as you
• Fraction Active - % population physically active as you

Derivation (From Drake's Equation)

In the 1961, Dr. Frank Drake created an equation to stimulate scientific dialogue on the topic of the search for extraterrestrial life.  He and several scientists, including the well known author Carl Sagan, used this equation to frame the important question of what is the probability that we could find a match for the conditions to support life elsewhere in the universe.  This Happiness Probability equation is based on the same principal.  Like Drake's Equation, this vCalc equation is meant to stimulate your own thoughts on how probable it is that you will find your match within your universe AND, morre importantly, to stimulate your thoughts on what realistically inhibits you finding that perfect match.

If we wanted to take this whole thought problem one step further, we could essentially append this Probability of Happiness equation to the Drake equation and thus challenge the universe to explain just how likely it is that we might find a person who bring us a happiest relationship from amongst the stars. 

Usage

Where to Start

In the Drake equation and this equation, the starting assumption is the size of the population from which you can reasonably assume you might find a match. The Drake equation makes assumptions of the number of stars in the galaxy first and the rate at which new stars are created.  You correspondingly must pick a value for the population in which you are likely to find a personality match. 

You have to ask yourself reasonably if you are going to encounter people from your local community, from the entire state, even from the entire country.  Are you willing to travel to meet the person you will share your life with.  My personal opinion is that this choice might decide out long-term happiness and therefore a little travel -- even a lot of travel -- is well worth it.  But that question probably deserves a study all its own -- whether it's possible to have a long distance relationship.

So, again, a basic premise of this equation is that you should start with an accurate and reasonable assumption about the population you are really willing to consider.  In the default settings, I used the population of a state. I believe I and many others would be wiling to consider people from a state-wide distribution and that travel about the state would not be considered overwhelming.  I often travel across the surrounding state for adventures and around the state for work-related activities, so why wouldn't I travel an hour to meet the girl of my dreams. This is exactly the kind of introspection this equations should conjure.

Considering the key factors also gives you some perspective, because if the numbers suggest that your perfect match is probably just a few people out of your entire state, you can more readily imagine how much time it will take to cover that dating ground.

What Else to Consider

First note, it is an easy thing to add your own factors to this equation.  vCalc provides the ability to all registered user to create their own equations and to add factors to this equation, all you have to do is push the button to duplicate the equation and add your own input factors.  Then you can save your own version and -- if you desire -- publish it to the world.

Now, let's start looking at the various factors included as inputs. You have to ask yourself if any of these differentiating attributes of a perfect match apply to your specific tastes and lifestyle desires.  If, for example, you consider yourself very political, then the Fraction Political input should probably be set to a low number -- which would mean you may have a difficult time finding  someone who is as politically motivated as you desire.  And since you may have difficulty living with someone who doesn't worry about politics the way you do, it may or may not be a factor you need to consider.

Remember, setting a factor to 1.0 basically takes it out of the equation because that means you expect the factor applies to the entire population.  In the Fraction Political example, setting the factor to 1.0 means you believe all the considered population will match you in your political nature.  If you are very strongly motivated by politics and political thought and you are using this equation realistically, you will set the Fraction Political input to a smaller number, meaning you expect there to be a smaller fraction of the population who matches you "politically".

The same thought process applies to each factor.  Set the fractional value to represent how much of the time or how likely it is that the person you're looking for will be within your target population.

Look at each input factor independently and ask:

• Is this important to me?
• If it's important how important is it?
• What is a reasonable way to estimate the fraction of the population that would meet my needs in this particular attribute?

What Are the Input Factors?

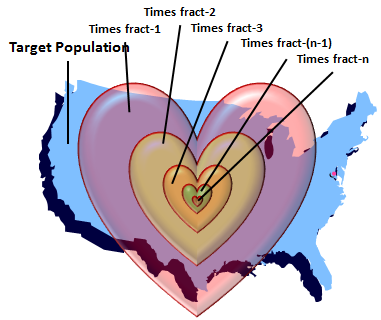
As the graphic depicts, the application of each additional input factor focuses your probability of finding a perfect match on a smaller and smaller segment of the target population until, when all factors are included, you see the relative size of the population of probable matches that would make you happy.  Remember this is a thought problem, like Drake's Equation, which is intended to help you think about all that goes into the probability of finding a perfect match.

The input factors considered are:

• Target Population - the size of the population in which you are willing to search.  This is probably the most important factor to consider since you can choose to have a direct affect on this factor in your choice to widen or limit the range of your search.

              As examples: the US population is around 318 million; the world population is around 7.2 billion; the population of Massachusetts is about 7 million; the population of the city of Phoenix is about 1.5 million. This equation defaults to the estimated population of Colorado in 2013, where I presently have cast my net. 

• Fraction Targeted Gender - the fraction of the population in the gender you prefer

              Assumed to be approximately 0.5 in most cases but it can vary by age.

• Fraction Single - the proportion of those in population that are single

              This input defaults to the US statistic of approximately 44% of the US population that are single.  If you have better data for your target population, change this value.  It varies significantly by age group so you may find statistics on age groups.

• Fraction May Encounter -- the fraction of the target population you chose that you may typically have a chance to encounter

              This factor defaults to the reported percentage that use on-line dating, so will be less if you date by encountering people in bars or other social settings. This is an important point to consider, which makes this equation so valuable as a thought problem.  If you choose the population of a large city to be your target population, then this input is the fraction of that city-size population you may likely meet. For most people, this fraction (ignoring on-line dating sites which bring people directly to you) is realistically very, very small.  Typically if you meet a hundred new people in a year you'd be zealously active.  And if your city size were a good round number of 1 million people, that would mean this input would be 0.0001.

So, what does that mean to you?  If you cannot justifiably think of an easy way to meet a lot of people, and you aren't using an on-line dating site, then you need to think about what this does to your chances of finding that perfect match. The math is talking to YOU. 

And I think the math is also explaining how so many people get married each year. If all those people getting married are meeting some very small number of the target population they live within, they must be lowering their expectations to have found the one they desire within that very,very small portion of the population.  Maybe there's more to it than that but the math kind of indicates that the Fraction May Encounter is the first and most limiting part of the equation.

• Fraction in Age Range - the fraction of the population that are in your preferred age range (see census site for US estimates; default is percentage males between 30 and 40)

If you are being realistic, you must consider this fraction to represent the age range percentage of the population you would be able to be comfortable with.  If you'd like a very much younger partner, you have to think about all that will imply about things which you will see so differently.

• Fraction Trustworthy - the fraction of the population that are trustworthy. Since a high percentage of relationship end in untrustworthy acts, this factor remains pretty important to people serious about long term relationships.  Since one statistic shows 30 to 60 percent will cheat on their spouse and since we assume the rate may be even higher for those in the dating phase of a relationship (because there is often a perception that it isn't as big a deal when  dating and not yet married), we chose the default for this value to be the high end of the range (60% are untrustworthy) and thus the applied percentage is 40% we can consider trustworthy and thus matching our desires. There are probably many studies on this topic from which you can get another value. If you consider this a very important factor to you, you might decrease this factor making the value reflect it is less likely to find someone trustworthy.

           This factor defaults to the max value in the range cited as the estimated number of people in the United states (roughly 30 to 60% of all married individuals (in the United States) will engage in infidelity at some point and the trustworthiness factor is then 1 - 0.60 = 0.40.

• Fraction Speak Your Language - the fraction of the population that speak the same language you do.  If you don't consider this an important factor then by all means you can set the value to 1.0, which again makes it a non-factor.

             Defaults to the census percentage of over 5 years old who speak only English at home: 0.7922

• Fraction Found Attractive -- a guesstimate of percentage of population you typically consider attractive.  I have set the default to a number that has been devised through research but which is not well substantiated: 13 %.  If you are real picky about physical beauty, you will want to set this value even lower.

• Fraction Find You Attractive -- a guesstimate of percentage of population which typically considers you attractive (we use again the 13 % as the default).  If you're a bit narcissistic you'll set this value much higher, implying most people find you attractive.  Being narcissistic in this case is not necessarily being unrealistic. Besides, most people tend to underestimate their own attractiveness.

• Fraction Intelligence - the fraction of the population that matches your intelligence expectations (defaults to percentage with college degree, 20.6% ).  Obviously if you don't have expectations of finding someone with a higher education you can set this factor to some value given by any realistic study.  The US percentage of high school graduates is about 88.15% so you could set the number to 0.8815 if you're not looking for a partner with a degree and think you could be quite happy with someone who has only a high school education.

• Fraction Political - the fraction of the target population who match your political tastes (defaults to the percentage moderates in the US)

• Fraction Religious - the fraction of the population which holds the same religious beliefs as you (defaults to fraction of the US who are Christian).  You could look-up the numbers for all the religions which don't offend you but realistically you have to consider what daily life would be like with someone with different religious views.  A safest bet  would be to set this value to the fraction of the population that has the same religious affiliation as you do.
  
  Which brings up an important consideration.  If I search on-line I can find an approximation for the number of, lets say, Jewish people in the United States. If I am Jewish I can get my Fraction Religious input factor by dividing that number of Jews in the country by the population of the US.  Wikipedia is nice enough to provide us with the factor so we don't have to divide ourselves, as it notes the Jewish percentage population of the united States is 0.0211 (2.11 %).  But note this averages this factor over the entire US and certainly there are fewer Jewish in many states, so you must have to think through the ways to estimate the percentage and then think also about what that means to your search.

• Fraction Funny - the fraction of the people you meet that you would consider funny enough to meet your needs (this subjective value defaults to 1/3). If you don't think funniness is important to you, you can set this factor to 1.0, which means that you expect all the target population to meet your humor expectations.  A very large percentage of women at on-line dating sites say they are looking for someone who makes them laugh and they also state this is very important to them.  I'm just guessing that in reality, on a daily basis, humor isn't as important a factor as the profiles from these sites imply.  Of course, I could be wrong. But, again, that's where the value in this equation lies.  You should be thinking about what it really means to you.
    
• Fraction Cuddle -- the fraction of the population that typically cuddles as much or as little as you desire (defaults to a value for cuddling a lot, estimated at 10%).  You can make your assumption on your own beliefs about how much people really do what is referred to as cuddling.  If you Google "cuddling in today's world" you'll find quite an assortment of sites focused on the topic, so the percentage may be higher than our estimated value.

• Fraction Sex - the fraction of the population you believe likes sex as much as you (defaults to 75% of women in my default estimate).  This is a pretty important factor, but if you think it isn't you can set you value to one, which basically nulls out the factor.

• Fraction Active - the fraction of the population who are about as physically active as you are, exercising and other activities (defaults to 30%)

My Interpretation of the results is that the probability is extremely low if you take into account just the factors outlined by the input variables.  In real life, there are many more things that might  influence your sense of the perfect match.  But if this discussion is valid, then it describes our contemporary experience with relationships quite well.  Few people look beyond their normal daily existence and so the starting population is much less than the population of the state of Colorado used as default here.  Yet the percentage of people who enter into a relationship is very much higher.  It leads me to theorize that one of the key contributing reasons for our greater than 50% divorce rate, and the additional unhappy relationships on top of that, may be due to most people ignoring many of these attributes.  When asked directly, they would acknowledge them as import to them but when entering into a relationship they have likely settled.  They have likely ignored many of these important-to-them attributes to artificially boost the chances they will find a "perfect match" -- right next door.

See also

This mathematical concept, as applied to happiness in relationships, has been talked about by at least two other people in exactly the same context.  I am happy to say this equation came first but here is a TED talk on the same subject and an article from Brain Pickings:

• What Mathematics Reveals About the Secret of Lasting Relationships and the Myth of Compromise
• Hannah Fry: The mathematics of love (a TED talk)

vCalc - Create, Collaborate, Calculate