This equation computes the force of gravity a body would experience at some distance inside a uniform density sphere.  In this case the mass of the sphere is assumed to be the mass of the Earth and so this is the force of the Earth's gravity experienced by a mass inside the Earth.

• r - the distance between the point mass (external to the sphere) and the center of the sphere
• M - the mass of the hollow sphere
• m - the mass of the point mass

The calculation returns the force `F_g` in Newtons by default.

Notes

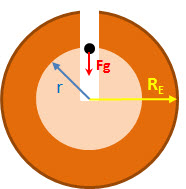
DERIVING THE EQUATION

If you were able to move a mass, m, into the interior of the earth to a point where it was a distance r from the center of the Earth, you'd find that the force of gravity experienced by the mass, m, is directly proportional to that distance from the center of the Earth.

      `F_g = ((G*m_E*m)*r)/R_E^3`, where m is the mass you have moved inside the Earth

You can derive two things directly from this computational knowledge:

1. If the mass were able to be taken to the center of the Earth, r would be zero and the force of gravity would also be zero.  In other words, at the center of the Earth the mass would be weightless.
2. At the surface of the Earth, `r = R_E` and therefore the equation simplifies to give us the force of gravity as we would expect at sea level: `F_g = (G*m_E*m)/R^2`

This hypothetical thought problem makes several gross assumptions, which include:

1. the Earth is a sphere (which is not true, as the Earth is slightly an oblate spheroid -- has bulges)
2. we treat the the mass of the Earth as uniform density sphere (when in fact there are regions internal to the Earth that are of higher density than others)

Note that the when the mass, m, is a distance in side the Earth, at a distance, r, from the center of the Earth, only the mass inside the sphere of radius r exerts a net gravitational force on the mass, m.  So, the effect of gravity inside a sphere is as if as you move closer to the center of the uniform density sphere, the mass effectively decreases as the distance from the center decreases.  Again, that means at the center of the Earth the mass effectively having a net gravitational force on the mass decreases to zero, so you experience zero gravity at the Earth's center.