Potential Energy - Point Mass Inside Spherical Shell
This equation computes the potential energy due to the gravitational attraction between a point mass and a spherical hollow shell mass when the point mass lies inside the spherical shell.
The inputs to this equation are:
- r - the distance between the point mass (external to the sphere) and the center of the sphere
- M - the mass of the hollow sphere
- m - the mass of the point mass
The calculation returns the potential energy, U.
Notes
DERIVING THE EQUATION
This is an interesting derivation to work through because it illustrates so clearly how to start such a geometry-laden problem from first principles, derive it in the calculus, and then in the end you find that the result displays a particularly unexpected simplicity. Physics likes to surprise like this -- a LOT.
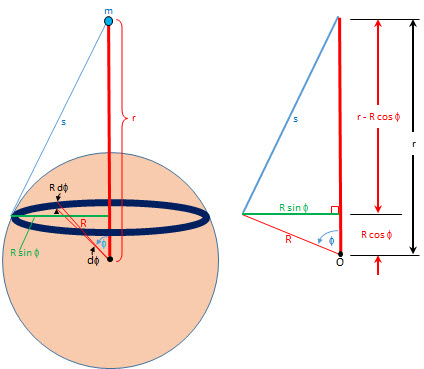
To derive the potential energy due to the gravitational interaction between a point mass and a hollow spherical mass, we first envision the mass of a small ring of matter symmetric about the axis drawn between the point mass and the center of the sphere. This ring is imagined to be comprised of many small particles of mass, mi. The line between the point mass, m, and the center of the sphere, O, has length r.
The potential energy of any particle of mass, mi, in this ring is given by:
[1] pg 401: Ui = -G⋅m⋅mis, where m is the mass of the point mass and s is the distance of the particle of mass, mi on the ring about the sphere to the point mass, m.
See the vCalc equation: Potential Energy of Gravity.
We're essentially going to try to integrate the potential energy across the sphere, which we visualize as summing up all the very thing rings of mass dM that comprise the whole sphere.
THE MASS OF A SINGLE RING AT DISTANCE s
We can determine the mass of the ring, dm, around the circle by summing these particles of mass: `dM = sum_i (m_i)` and using this the potential energy of interaction between the ring of particles and the point mass, m, becomes:
[1] eq. 12.18 `dU = ( -G*m*dM)/s`
See the vCalc equation: Potential Energy of due to Gravitational Attraction.
To compute the potential energy of the interaction of the whole sphere and the point mass, we need to know the mass of any ring of mass. We can then integrate over the angle theta, basically summing the potential energy of all the stacked rings of mass that comprise the sphere. Since the radius of the shell sphere is R, we know the radius of any ring on the shell sphere is R⋅sin(θ) and the ring's circumference is:
[1] pg 401: 2⋅π⋅R⋅sin(θ). (See Ring Circumference On Sphere)
The width of any ring that comprises the sphere, as shown in the picture, is R⋅dthη and therefore the area of the ring is then approximately the product of the ring's width times the ring's circumference:
[1] pg 401: dA=2⋅π⋅R2⋅sin(θ)⋅dthη
Since we are assuming a sphere of uniformly distributed mass, the following ratio is given:
[1] pg 401: `dM / M = dA / A`
Which then gives us by substitution:
[1] eq. 12.19: dMM=12sin(θ)dthη
THE POTENTIAL OF ANY COMPONENT RING OF MASS
Solving this equation for dM and substituting it into eq 12.18 above we get:
[1] eq. 12.20: `dU = (-G*M*m* sin(theta) dtheta) / 2s
This is the potential energy of the interaction of any of the stacked horizontal rings with the point mass. Integrating this over the sphere will give us the total potential energy between the sphere and the point mass. Now since s we can see that s is the hypotenuse of a right triangle whose sides are (r-R⋅cos(θ)) and R⋅sin(θ), we can compute s2:
[1] eq.12.21: s2=r2-2⋅r⋅R⋅cos(θ)+R2 (see Distance to Point of Ring On Sphere)
Taking the derivative of eq12.21 gives us:
[1] pg401: s⋅ds=r⋅R⋅sin(θ)⋅dthη
Substituting into equation 12.20 above, we can rearrange to get"
[1] eq. 12.22; dU=(-G⋅M⋅m2⋅r⋅R)⋅ds
INTEGRATING OUR FORMULATION
Integrating this last equation from s = R-r to s = r+R gives us the total potential energy of the gravitational interaction between a point mass, m, and a hollow sphere of mass M when m lies inside the sphere:
[1] eq 12.23: U = -G⋅M⋅m2⋅r⋅R [ (r + R) - (R - r) ]
And finally this equation, eq. 12.23, simplifies to:
[1] eq. 12.24: U= -G⋅M⋅mR
That is surely an amazing bit of differential and integral math to come up with a very simple equation for the gravitational potential energy exhibited between a point mass and a spherical hollow mass. Even more amazing is that the potential energy, U, can be computed by treating both the point mass and the sphere as point masses. This turns out to hold for both the point mass being inside or outside the shell!
Equations and Data Items
- Comments
- Attachments
- Stats
No comments |
