Max Range and Height and Flight Time

The Max Ballistic Range, Height and Time calculator computes the maximum range (horizontal distance), height (vertical distance) traveled and travel time by an object based on the initial velocity (V) of the object, and angle of launch (θ), the launch point's height (h) above the plane, and the acceleration due to gravity (g).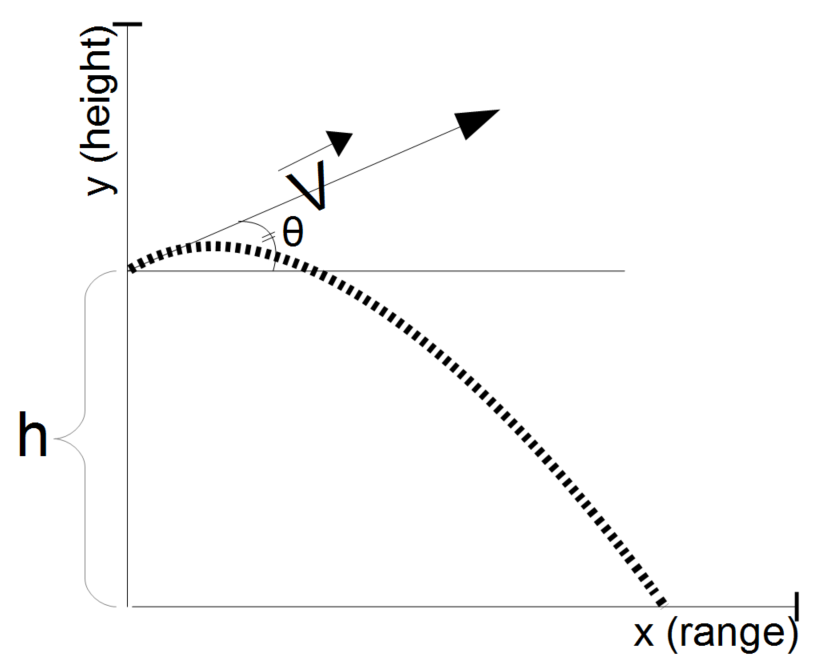

INSTRUCTIONS: Choose units and enter the following:

• (V)  Initial velocity (e.g. muzzle velocity from the gun or cannon)
• (θ)  Launch angle above the horizon.
• (h)  Initial height of the launch point above the plane.
• (g)  Acceleration due to gravity with a default of  9.80665 m/s² 

Max Range, Height and Time (Mx): The calculator returns the:

• (R) Maximum Range in meters. 
• (MxH) Maximum Height in meters, and 
• (t) Travel Time in seconds.

 However, these can be automatically converted to compatible units via the pull-down menu.

The Math / Science

The Maximum Ballistic Range equation is:

     `r = ((V • sinθ + sqrt( (V •sinθ)² + (2•g•h))) / g) • cosθ•V`

The formula for Max Ballistic Height  is:

      h = (V • sin(θ))² / (2•g)

The formula for the Ballistic Travel Time is:

     `t = (V sinθ + sqrt( (V sinθ)^2 + 2gh))/g`

where:

• r = max ballistic range
• h = maximum height.
• t = total ballistic flight travel time
• V = initial velocity
• θ = launch angle
• h = height or elevation above the plane
• g = acceleration due to gravity

Acceleration Due to gravity

The force of gravity pulls masses towards each other.  In the case of small objects (e.g. you, an arrow or the Space Shuttle) verses planetary objects (e.g. the Earth or Moon), the difference in masses result in a negligible acceleration of the large object toward the small and small object accelerating toward the center of mass of the large object.  Acceleration due to gravity changes based on the mass of the object (e.g. the Earth 9.8 m/s² verses the moon1.6 m/s²) and the distance from the center of mass.  For example, since the Earth is not a perfect sphere, and more closely represented as an oblate spheroid, acceleration due to Earth gravity as Sea Level is more accurately calculated based on latitude: click here -> The international gravity formula provide an acceleration due to gravity based on latitude.  CLICK HERE for the acceleration due to gravity for the other planets in the solar system. 

Ballistic Flight Equations and Calculators

• Ballistic Maximum Altitude:  This is the maximum altitude achieved in free ballistic flight.
• Ballistic Maximum Range:  This is the maximum horizontal range.
• Ballistic Flight Time:  This is the time duration of free flight.
• Ballistic Position: This computes the X,Y position at a given time.
• Ballistic Vertical Velocity: This is the vertical velocity at a given time.
• Ballistic Horizontal Velocity: This is horizontal velocity or ground speed.
• Vertical Position in Ballistic Flight: This compute the vertical position (y) at a given time within ballistic flight.
• Horizontal Position in Ballistic Flight: This compute the horizontal position (x) at a given time within ballistic flight.
• Velocity to achieve a Max Ballistic Height: This computes the initial velocity required to achieve the max height.

• Travel Time
• International Gravity Equation
• Force of Earth's Gravity
• Force of Drag