Torque Free Ratio of Ellipsoid Spin to Precession
a | ||
b | ||
theta | ||
The Torque Free Ratio of Ellipsoid Spin to Precession equation computes the torque free spin-to-wobble (aka spin-to-precession) ratio for an ellipsoid. This ratio can be used as a measure of the stability of the motion of an ellipsoid spinning about the major axis.
A common example of this ratio can be used to understand why the mechanics of a football pass dictates that putting spin on the ball has the effect to cause the ball to travel smoothy with little wobble.
Derivation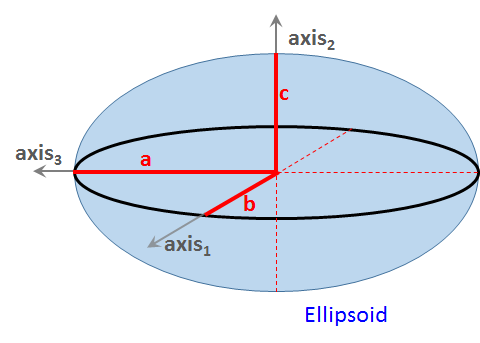
Eq. 1: spinprecession=ω3.ϕ=I1⋅cos(θ)I3=12(1+a2b2)cos(θ), where
- I1 is the moment of inertia about the cross axes, axis1. (Note that axis1 = axis2.)
- I3 is the moment of inertia about the long axis of the ellipsoid, axis3.
- a is the semi-major axis of the ellipsoid (half the length of the ellipsoid).
- b is the semi-minor axis of the ellipsoid (half the length of the cross dimension). Note b=c because the cross section is a circle and therefore b & c are radii.
- θ is the angle between the moment of inertia direction and the symmetry axis (axis3).
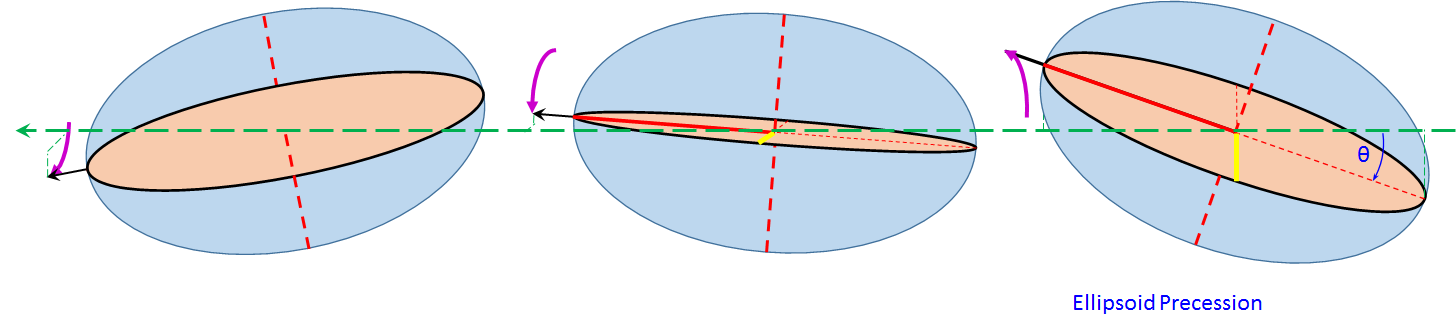
Usage
Since the ellipsoid is a good approximation for the shape of a football, this computation is a good approximation of the spin-to-wobble ration of a well thrown pass. This indicator of stability (the spin-to-wobble ratio) can predict the amount of wobble one might expect when throwing a spiral pass.
From Eq. 1 we see that the wobble-to- spin ratio (the inverse of the spin-to-wobble ratio) when length a approaches length b.
cos(θ)=2⋅spinprecession1+a2b2 =>
θ=arccos(2⋅spinprecession1+a2b2)
This implies the angle of the wobble (precession) is minimized when a approaches b. In other words, the wobble decreases as the ellipsoid comes closer to being a sphere. This also implies the angle of the wobble increases as spin tends toward zero. This is kind of intuitive, as a football passed without spin tends to wobble a lot.
1
