For a circle whose center, C, lies on the y-axis and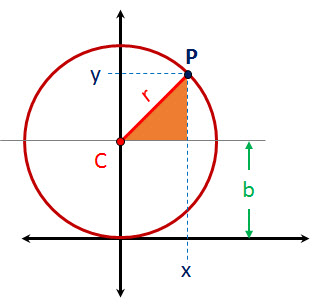  Circle on Y axis  for which the Cartesian origin is on the circle, this equation computes the absolute value of the x-coordinates of a point on a circle given the y-coordinate, y, and the radius of the circle, r (see diagram). 

Because of the symmetry of this particular circle's location with its center on the y-axis, there is always a plus-x and minus-x point corresponding to each y value (except when y = 0 or y = `2*r`).  Take a look at the diagram and verify this for yourself.

Notes

This depiction of a circle defined in a Cartesian coordinate system has a radius, r. This circle also has its center defined to be at the point on the y-axis (0,b), where b is equal to r.  An arbitrary point on the circle is defined to be at a point, P(x, y) .

Since the y-axis passes through the circle's center, the circle is symmetric about the y-axis and so we expect to find that there are two values of x for every corresponding value of y, except for the points on the circle that are also on the y-axis (where x is precisely zero).  As we derive the equation, the math will confirm this assumption.

First, we note  that the radius is the hypotenuse of the right triangle shown in orange whose other two sides have dimensions x and (y - b), so by the Pythagorean Theorem tells us: r² = x² + (y-b)²

If we simply solve this for x, we'll get a formula for the pair of x-coordinates symmetrically displaced about the y-axis.

r² = x² + (y - b)²

rearranging: x² = r² - (y - b)²

then  x = `+- sqrt(r^2 - (y - b)^2)`

we substitute the length of r for b, since again the center of the circle is defined to at y = b = r.

then  x = `+- sqrt(r^2 - (y - r)^2)`

Notice that when y = 0, x = 0, so the equation confirms that the origin is a point on the circle.

Notice also that when y = `2*r`,  x is again zero.