Tags | |
The Monthly Interest Rate calculator computes the monthly interest rate for a fixed rate loan.
INSTRUCTIONS: Choose the preferred currency units and enter the following:
- (P) This is the original principal of the loan
- (N) This is the duration of the loan
- (Pmt) This is the monthly payment amount
Monthly Interest Rate: The calculator return the monthly % interest rate.
Related Calculators:
- Annual Interest Rate: : This computes the annual interest rate on a fixed rate loan based on the monthly payment, duraton of the loan and principal amount.
- Monthly Payment: : This computes the monthly payment on a fixed rate loan based on the annual interest rate, duraton of the loan and principal amount.
The Math / Science
A loan which has a fixed interest rate, r, and N equal monthly payments of the amount, Paymnt, can be characterized by the equation:
P⋅r=Paymnt⋅(1-1(1+r)N )
Rearranging we can define: f(r)=PPaymnt⋅r+1(1+r)N -1
Setting f(r)=0 to find the roots of this function, we can now use the iterative Newton Raphson Method to find the monthly interest rate, r. 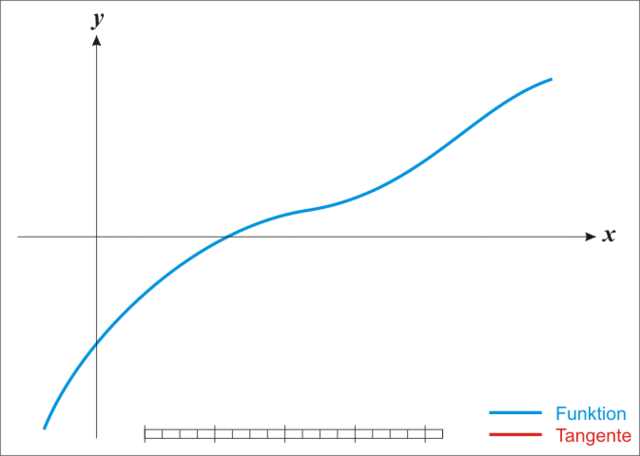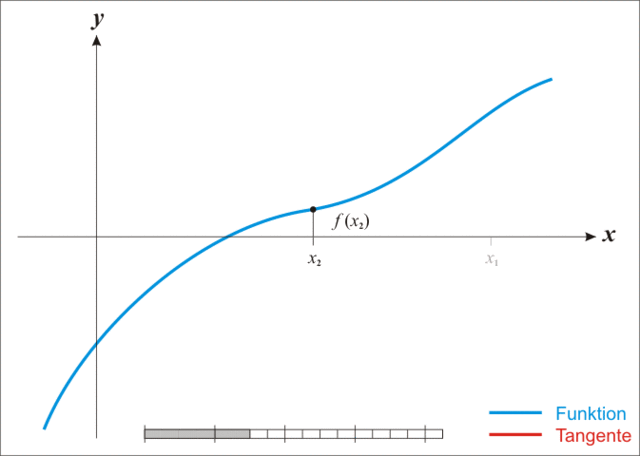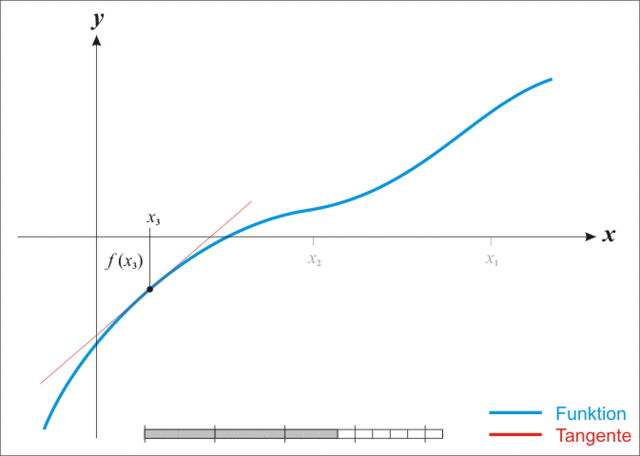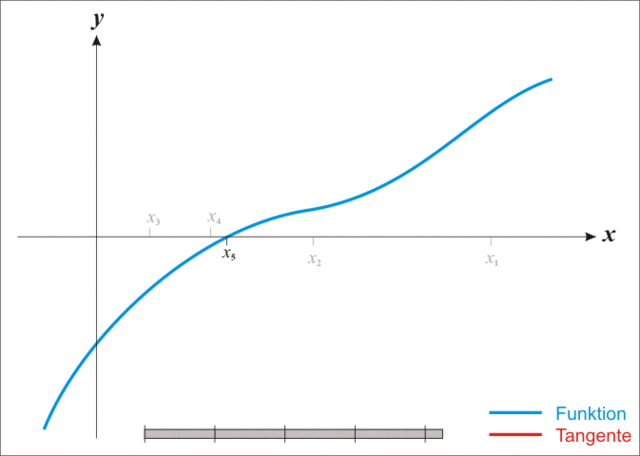
Newtonian Iteration Animation, Wikipedia / Ralph Pfeifer
CC BY-3.0
Newton Raphson Method1
The Newton Raphson Method is an iterative numerical analysis method for finding the roots of a real-value function. We want to find in this case the interest rate, r, that is where f(r)=0.
The Newton Raphson Method makes successively better approximations of the value of r by using the derivative of f(r), which we denote f′(r), to define the tangent at the point [rn,f(rn)]. Each successive approximation uses the tangent thus derived for rn, which will intersect the x-axis at the next value rn+1.
If we pick a first guess interest rate, r0, the Newton Raphson Method tells us that a next better approximation is given as follows:
r1=r0-f(r0)f′(r0)
If we look at the example graph at the right of the function, f(x), the x-value approximation where the function crosses the x-axis at x1 is the intersection with the x-axis of the tangent to the graph which touches the curve f(x) at the point (x0,f(x0)).
The Newton Raphson Method generalizes the successive better approximations of the function's root (where the function intersects the x-axis) with the following equation:
xn+1=xn-f(xn)f′(xn) This equation iterates over some number of successive approximations of xn+1 and arrives quickly at a very close approximation of the interest rate, rn+1.

