The Rate of a Reaction
From UCDavis Chemwiki and UCDavis Chemwiki link two.
The Reaction Rate for a given chemical reaction is the measure of the change in concentration of the reactants or the change in concentration of the products per unit time.
During the course of the reaction shown below, reactants A and B are consumed while the concentration of product AB increases. The reaction rate can be determined by measuring how fast the concentration of A or B decreases, or by how fast the concentration of AB increases.
`A+B->AB`
.jpg)
Figure 16.1.1. The above picture shows a hypthetical reaction profile in which the reactants (red)
decrease in concentration as the products increase in concetration (blue).
For a description of the figure, click on the figure.
For the stochiometrically complicated Reaction:
`aA + bB -> cC + dD`
Rate `= (-1)/(a) (d[A])/(dt) = (-1)/(b) (d[B])/(dt) = (-1)/(c) (d[C])/(dt) = (-1)/(d) (d[D])/(dt)`
Looking at Figure 16.1.1 above, we can see that the rate can be measured in terms of either reactant (A or B) or either product (C or D). Not all variables are needed to solve for the rate. Therefore, if you have the value for "A" as well as the value for "a" you can solve for the reaction rate.
You can also notice from Formula 1 above that, the change in reactants over the change in time must have a negative sign in front of them. The reason for this is because the reactants are decreasing as a function of time, the rate would come out to be negative (because it is the reverse rate). Therefore, putting a negative sign in front of the variable will allow for the solution to be a positive rate.
Coefficients in Reaction Rates
Consider the reaction
`2 N_2O_5(g) -> 4 NO_2(g) + O-2(g)`
According to stoichiometry, two molecules of N2O5 must disappear for every one molecule of O2 that is formed. And for every mole of O2 formed, there must be four moles of NO2 formed. Thus NO2 is formed four times as fast as O2, and N2O5 disappears twice as fast as O2 appears. If we define the rate in terms of the change in concentration of NO2per unit time, then the rate will be four times faster than if we define the rate in terms of the change in concentration of O2. Similarly, the rate of disappearance of N2O5 will be twice as great as the rate of appearance of O2.
Having the rate of reaction differ depending on which substance we consider could cause a lot of confusion. Therefore, by convention, the rate is defined in a way that always gives the same value. This is done by multiplying the appropriate derivative by the reciprocal of the coefficient in the balanced chemical equation. For the reaction above, the rate is defined as,
Rate `= -1/2 (d[N_2 O_5])/(dt) = 1/4 (d[NO_2])/(dt) = 1/1 (d[O_2])/(dt)`
Although N2O5 is disappearing twice as fast as O2 is forming (that is, d[N2O5]/dt is twice d[O2]/dt), multiplying d[N2O5]/dt by the factor 1/2 and changing its sign insures that the rate has the same value. Similarly, even though d[NO2]/dt is four times as great as d[O2]/dt, the factor of 1/4 makes the rate the same.
In order think meaningfully about these different rates of reaction, the rate needs to be quantified. This can be done for reactions in solution by looking at the dependence of concentration of a reactant or product when considering time. Figure 16.1.2 displays a decomposition reaction of dye into colorless chemicals at two different temperatures, giving dye concentration at different times.
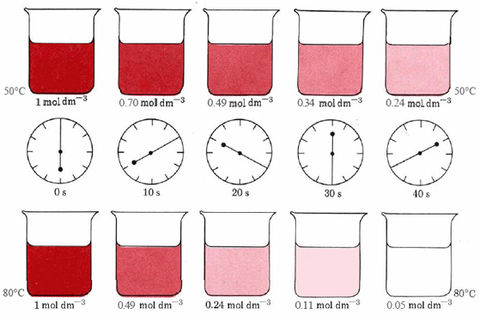
Figure 16.1.2 The decomposition of a colored dye at two different temperatures. The color of the solution fades gradually because the concentration of then dye decreases with time. The more gradual fading of the color at 50°C indicates that the dye decomposes more slowly at this temperature. How slow or fast a reaction is measured by the rate at which the concentration changes with time.
As the dye decomposes, its concentration decreases and the color of the solution becomes fainter. This happens in a shorter time at 80°C than at 50°C, indicating that the dye decomposes faster at the higher temperature. By convention, then, the rate of the reaction is described in terms of the change in concentration per unit time for a reactant or product. The faster that concentration changes, the faster the reaction is going.
As an example of the use of this definition of reaction rate, consider the first 10 s during decomposition of the dye at 50°C. According to Fig. 1 the concentration of dye drops to 0.70 mol dm–3 from an initial value of 1.0 mol dm–3. If we represent the change in the concentration of the reactant dye by `Deltac_R`, then
`Deltac_R = c_1 – c_2 = (0.70 – 1.00) "mol dm"^(-3) = – 0.30 "mol dm"^(-3)`
In other words the concentration of dye has decreased by 0.30 mol dm–3. We can calculate an average rate of reaction by dividing this concentration decrease by the time interval (`Deltat = t_2 – t_1 = 10 s – 0 s = 10 s`) during which it occurred:
Average rate `= 0.30 "mol dm"^(-3) 10^(-1) s^(-1) = 0.03 "mol dm"^(-3) s^(-1)`
Clearly, no matter what reactant we observe, its concentration will decrease with time and `Deltac_R` will be negative. On the other hand, the concentration of a reaction product will always increase, and so `Deltac_P` will always be positive. Since we want the average reaction rate always to be positive, we define it as
Rate `= (-Deltac_R)/(Deltat)`
EXAMPLE 1
Using the reaction shown in Example 1, calculate the reaction rate from the following data taken at 56°C:
| `2N_2O_5(g) -> 4NO_2(g) + O_2(g)` | |||
|---|---|---|---|
| Time (s) | [`N_2O_5`] (M) | [`NO_2`] (M) | [`O_2`] (M) |
| 240 | 0.0388 | 0.0314 | 0.00792 |
| 600 | 0.0197 | 0.0699 | 0.0175 |
This example illustrates two important points about reaction rates. The first is that the rate of a reaction usually decreases with time, reaching a value of zero when the reaction is complete. This is usually because the rate depends in some way on the concentrations of one or more reactants, and as those concentrations decrease, the rate also decreases. The second point is a corollary to the first. Because the reaction rate changes with time, the rate we measure depends on the time interval used. For example, the average rate over the period to 30 s was 0.030 mol dm–3s–1, but the average rate over the middle 10 s of that period was 0.025 mol dm–3 s–1. The different average for the 30-s interval reflects the fact that the rate dropped from 0.051 to 0.013 mol dm–3 s–1 during that period.
The derivative also gives the slope of the tangent to a graph of versus t. Such a graph is shown in Fig. 2, with a tangent line drawn at t = 15 s. The slope of this line is – 0.0245 dm–3 s–1, giving
This exact value is quite close to the average rate of 0.025mol mol dm–3 s–1 calculated for the interval 10 to 20 s, but it is farther from the 0.030 mol dm–3 s–1 calculated over the 0 to 30-s interval. As expected, the larger the time interval, the less accurate the calculated rate.
This Collection is empty
- Comments
- Attachments
- Stats
No comments |
