Qualitative Description of Acid–Base Equilibriums

We now turn our attention to acid–base reactions to see how the concepts of chemical equilibrium and equilibrium constants can deepen our understanding of this kind of chemical behavior. We begin with a qualitative description of acid–base equilibriums in terms of the Brønsted–Lowry model and then proceed to a quantitative description in the next section"Quantitative Aspects of Acid–Base Equilibriums".

Conjugate Acid–Base Pairs

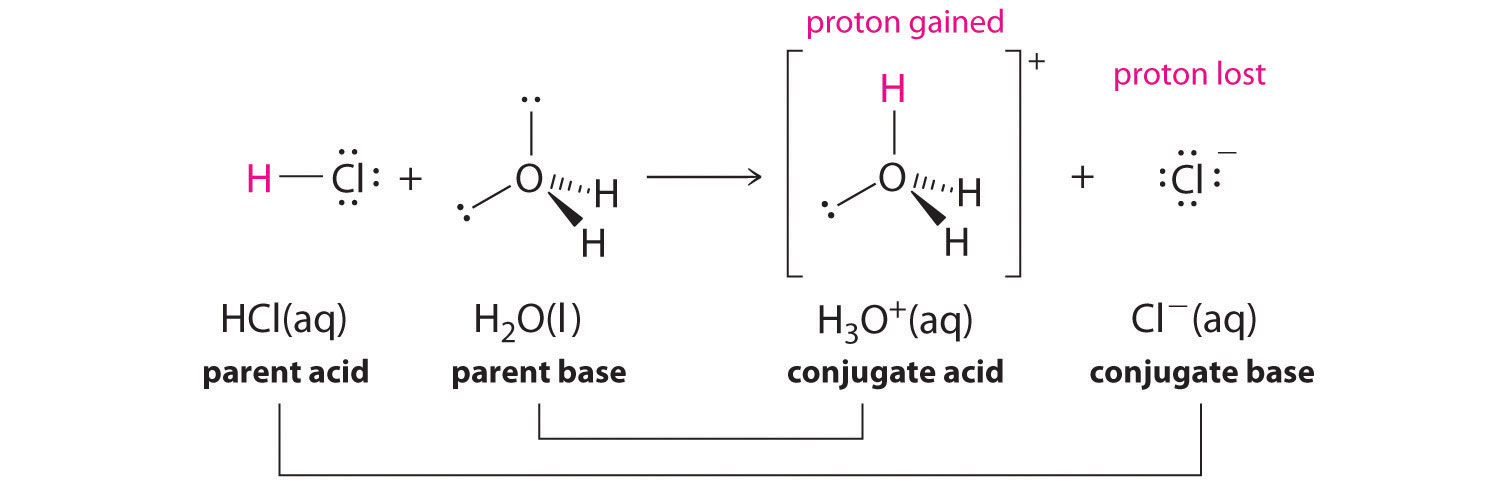
We discussed the concept of conjugate acid–base pairs in a previous section, using the reaction of ammonia, the base, with water, the acid, as an example. In aqueous solutions, acids and bases can be defined in terms of the transfer of a proton from an acid to a base. Thus for every acidic species in an aqueous solution, there exists a species derived from the acid by the loss of a proton. These two species that differ by only a proton constitute a conjugate acid–base pair. For example, in the reaction of HCl with water, HCl, the parent acid, donates a proton to a water molecule, theparent base, thereby forming Cl^-. Thus HCl and Cl^- constitute a conjugate acid–base pair. By convention, we always write a conjugate acid–base pair as the acid followed by its conjugate base. In the reverse reaction, the Cl^- ion in solution acts as a base to accept a proton from H₃O⁺, forming H₂O and HCl. Thus H₃O⁺ and H₂O constitute a second conjugate acid–base pair. In general, any acid–base reaction must contain two conjugate acid–base pairs, which in this case are HCl/Cl^- and H₃O⁺/H₂O.

Note the Pattern

All acid–base reactions contain two conjugate acid–base pairs.

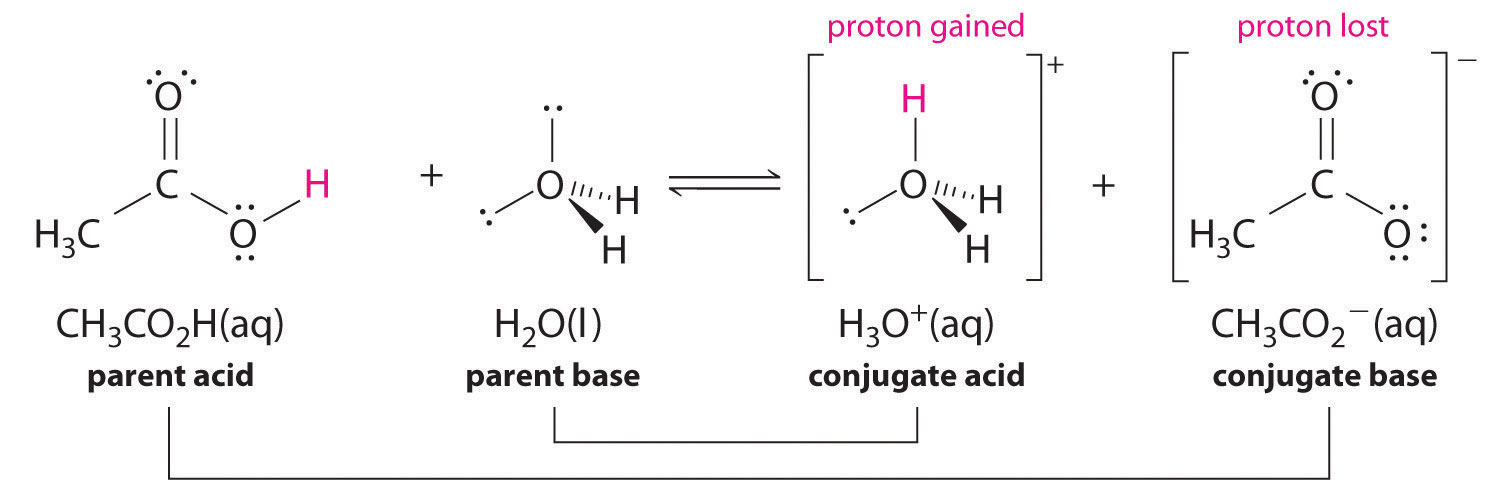
Similarly, in the reaction of acetic acid with water, acetic acid donates a proton to water, which acts as the base. In the reverse reaction, H₃O⁺ is the acid that donates a proton to the acetate ion, which acts as the base. Once again, we have two conjugate acid–base pairs: the parent acid and its conjugate base (CH₃CO₂H/CH₃CO₂^-) and the parent base and its conjugate acid (H₃O⁺/H₂O).

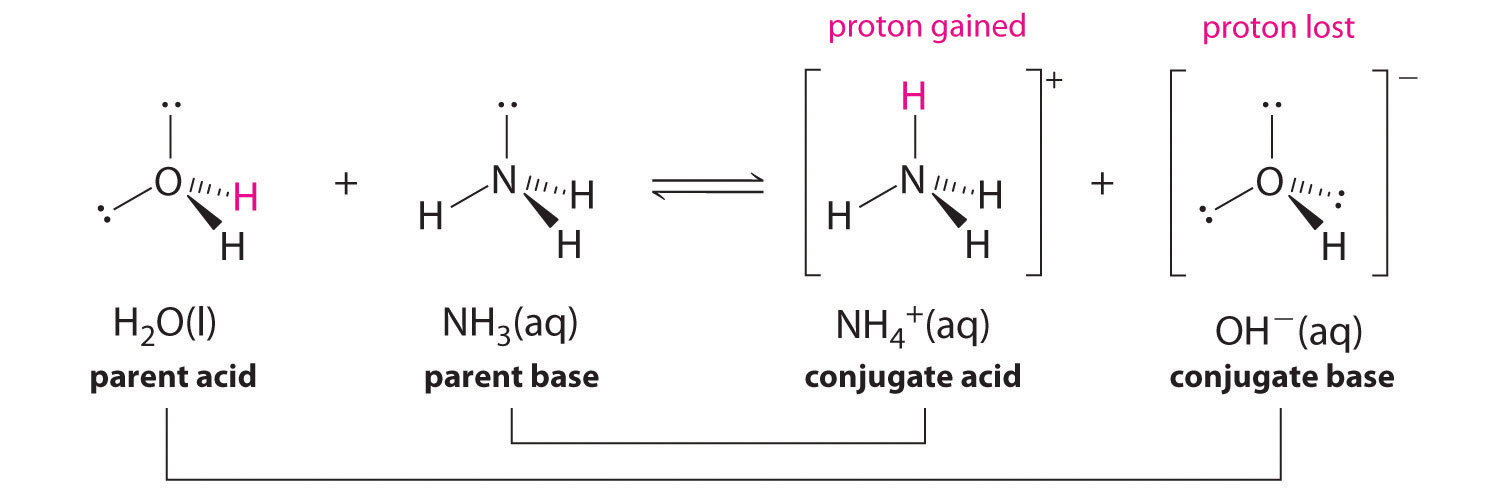
In the reaction of ammonia with water to give ammonium ions and hydroxide ions (Equation 16.3), ammonia acts as a base by accepting a proton from a water molecule, which in this case means that water is acting as an acid. In the reverse reaction, an ammonium ion acts as an acid by donating a proton to a hydroxide ion, and the hydroxide ion acts as a base. The conjugate acid–base pairs for this reaction are NH₄⁺/NH₃ and H₂O/OH^-. Some common conjugate acid–base pairs are shown here.

The Relative Strengths of Some Common Conjugate Acid–Base Pairs

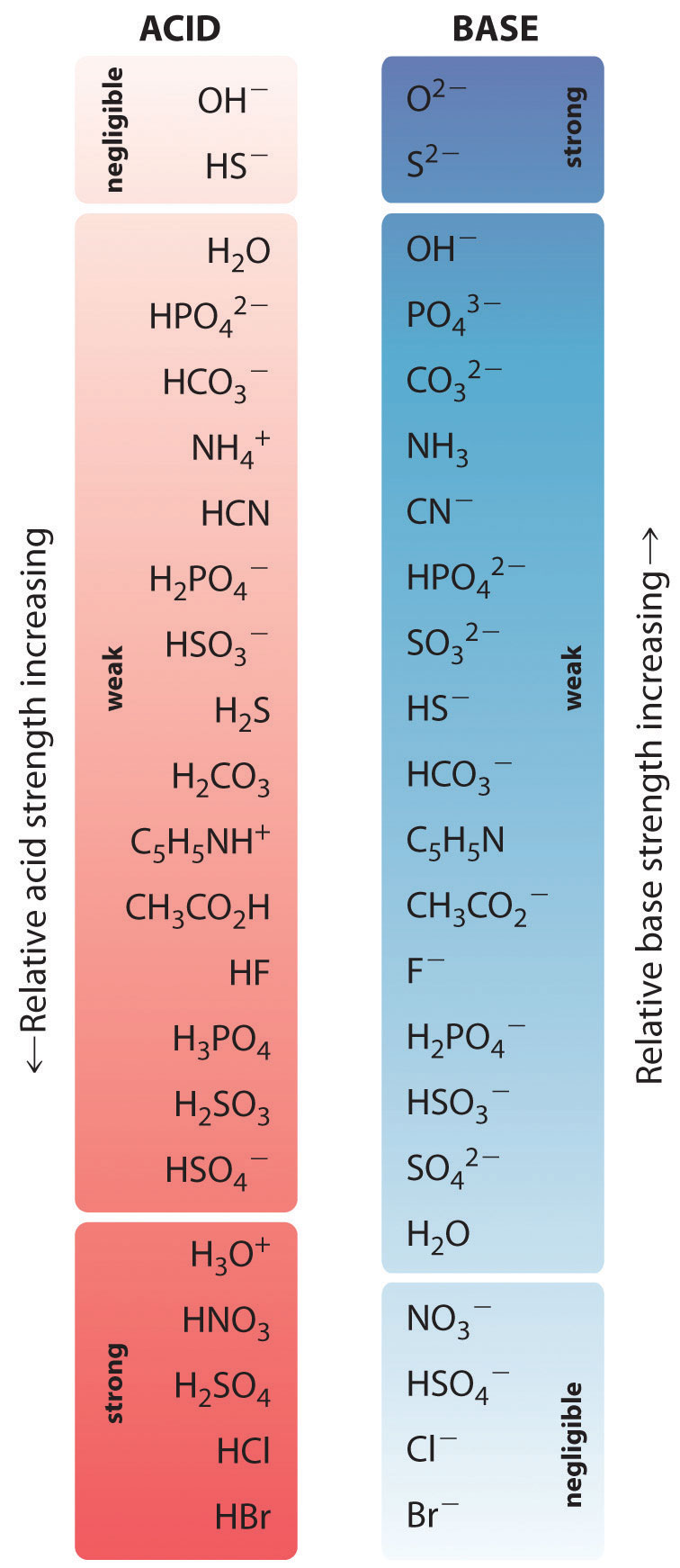
]The strongest acids are at the bottom left, and the strongest bases are at the top right. The conjugate base of a strong acid is a very weak base, and, conversely, the conjugate acid of a strong base is a very weak acid.

Acid–Base Equilibrium Constants: K_a, K_b, pK_a, and pK_b

The magnitude of the equilibrium constant for an ionization reaction can be used to determine the relative strengths of acids and bases. For example, the general equation for the ionization of a weak acid in water, where HA is the parent acid and A^- is its conjugate base, is as follows:

Thus the numerical values of K and K_a differ by the concentration of water (55.3 M). Again, for simplicity, H₃O⁺ can be written as H⁺. Keep in mind, though, that free H⁺ does not exist in aqueous solutions and that a proton is transferred to H₂O in all acid ionization reactions to form H₃O⁺. The larger the K_a, the stronger the acid and the higher the H⁺concentration at equilibrium.Like all equilibrium constants, acid–base ionization constants are actually measured in terms of the activities of H⁺ or OH^-, thus making them unitless. The values of K_a for a number of common acids are given in the following table.

Values of K_a, pK_a, K_b, and pK_b for Selected Acids (HA) and Their Conjugate Bases (A^?)

Acid	`HA`	`K_a`	`pK_a`	`A^-`	`K_ b`	`pK_b`
hydroiodic acid	`HI`	`2 × 10^9`	`-9.3`	I^(-)	`5.5 × 10^(-24)`	`23.26`
sulfuric acid (1)*	`H_2 SO_4`	`1 × 10^2`	`-2.0`	`HSO_4^(-)`	`1 × 10^(-16)`	`16.0`
nitric acid	`HNO_3`	`2.3 × 10^1`	`-1.37`	`NO_3^(-)`	`4.3 × 10^(-16)`	`15.37`
hydronium ion	`H_3O^(+)`	`1.0`	`0.00`	`H_2O`	`1.0 × 10^(-14)`	`14.00`
sulfuric acid (2)*	`HSO_4^(-)`	`1.0 × 10^(-2)`	`1.99`	`SO_4^(2-)`	`9.8 × 10^(-13)`	`12.01`
hydrofluoric acid	`HF`	`6.3 × 10^(-4)`	`3.20`	`F^(-)`	`1.6 × 10^(-11)`	`10.80`
nitrous acid	`HNO_2`	`5.6 × 10^(-4)`	`3.25`	`NO_2^(-)	`1.8 × 10^(-11)`	`10.75
formic acid	`HCO_2H`	`1.78 × 10^(-4)`	`3.750`	`HCO_2^(-)`	`5.6 × 10^(-11)`	`10.25`
benzoic acid	`C_6 H_5CO_2H`	`6.3 × 10^(-5)`	`4.20`	`C_6 H_5 CO_2^(-)`	`1.6 × 10^(-10)`	`9.80`
acetic acid	`CH_3CO_2H`	`1.7 × 10^(-5)`	`4.76`	`CH_3 CO_2^(-)`	`5.8 × 10^(-10)`	`9.24`
pyridinium ion	`C_5H_5NH^(+)	`5.9 × 10^(-6)`	`5.23`	`C-5 H_5 N`	`1.7 × 10^(-9)`	`8.77`
hypochlorous acid	`HOCl`	`4.0 × 1^(-8)`	`7.40`	`OCl^(-)`	`2.5 × 10^(-7)`	`6.60`
hydrocyanic acid	`HCN`	`6.2 × 1^(-10)`	`9.21`	`CN^(-)`	`1.6 × 10^(-5)`	`4.79`
ammonium ion	`NH_4^(+)`	`5.6 × 1^(-10)`	`9.25`	`NH_3`	`1.8 × 10^(-5)`	`4.75`
water	`H_2O`	`1.0 × 1^(-14)`	`14.00`	`OH^(-)`	`1.00`	`0.00`
acetylene	`C_2H_2`	`1 × 1^(-26)`	`26.0`	`HC_2^(-)`	`1 × 10^(12)`	`-12.0`
ammonia	`NH_3`	`1 × 1^(-35)`	`35.0`	`NH_2^(-)`	`1 × 10^(21)`	`-21.0`
*The number in parentheses indicates the ionization step referred to for a polyprotic acid.

Weak bases react with water to produce the hydroxide ion, as shown in the following general equation, where B is the parent base and BH⁺ is its conjugate acid:

Once again, the concentration of water is constant, so it does not appear in the equilibrium constant expression; instead, it is included in the K_b. The larger the K_b, the stronger the base and the higher the OH^- concentration at equilibrium. The values of K_b for a number of common weak bases are given in the following table.

Values of K_b, pK_b, K_a, and pK_a for Selected Weak Bases (B) and Their Conjugate Acids (BH⁺)

Base	B	K b	pKb	BH+	K a	pKa
hydroxide ion	`OH^(-)	`1.0`	`0.00*`	`H_2O`	`1.0 × 10^(-14)`	`14.00`
phosphate ion	`PO_4^(3-)`	`2.1 × 10^(-2)`	`1.68`	`HPO_4^(2-)`	`4.8 × 10^(-13)`	`12.32`
dimethylamine	`(CH_3)_2 NH`	`5.4 × 10^(-4)`	`3.27`	`(CH_3)_2NH_2^(+)`	`1.9 × 10^(-11)`	`10.73`
methylamine	`CH_3NH_2`	`4.6 × 10^(-4)`	`3.34`	`CH_3NH_3^(+)`	`2.2 × 10^(-11)`	`10.66`
trimethylamine	`(CH_3)_3N`	`6.3 × 10^(-5)`	`4.20`	`(CH_3)_3NH^(+)	`1.6 × 10^(-10)`	`9.80`
ammonia	`NH_3`	`1.8 × 10^(-5)`	`4.75`	`NH_4^(+)`	`5.6 × 10^(-10)`	`9.25`
pyridine	`C_5 H_5 N`	`1.7 × 10^(-9)`	`8.77`	`C_5 H_5NH^(+)`	`5.9 × 10^(-6)`	`5.23`
aniline	`C_6 H_5 NH_2`	`7.4 × 10^(-10)`	`9.13`	`C_6 H_5NH_3^(+)`	`1.3 × 1)^(-5)`	`4.87`
water	`H_2O`	`1.0 × 10^(-14)`	`14.00`	`H_3O^(+)`	`1.0*`	`0.00`

There is a simple relationship between the magnitude of K_a for an acid and K_b for its conjugate base. Consider, for example, the ionization of hydrocyanic acid (HCN) in water to produce an acidic solution, and the reaction of CN^? with water to produce a basic solution:

`HCN (aq) ? H^(+) (aq) + CN^(-) (aq)`     Equation 1

`CN^(-) (aq) + H_2 O(l) ? OH^(-) (aq) + HCN (aq)`     Equation 2

The equilibrium constant expression for the ionization of HCN is as follows:

`K_a = ([H^(+)][CN^(-)])/([HCN])`     Equation 3

The corresponding expression for the reaction of cyanide with water is as follows:

`K_b = ([OH^(-)][HCN])/([CN^(-)])`     Equation 4

If we add Equation 16.19 and Equation 16.20, we obtain the following:

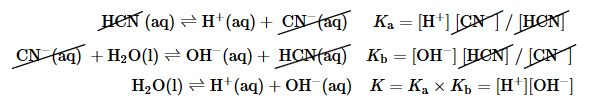
In this case, the sum of the reactions described by K_a and K_b is the equation for the autoionization of water, and the product of the two equilibrium constants is K_w:

Equation 16.23

K_aK_b = K_wThus if we know either K_a for an acid or K_b for its conjugate base, we can calculate the other equilibrium constant for any conjugate acid–base pair.

Just as with pH, pOH, and pK_w, we can use negative logarithms to avoid exponential notation in writing acid and base ionization constants, by defining pK_a as follows:

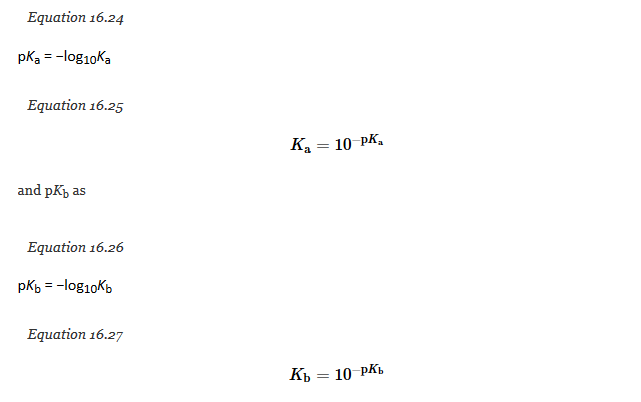
Similarly, Equation 16.23, which expresses the relationship between K_a and K_b, can be written in logarithmic form as follows:

Equation 16.28

pK_a + pK_b = pK_wAt 25°C, this becomes

Equation 16.29

pK_a + pK_b = 14.00The relative strengths of some common acids and their conjugate bases are shown graphically in the figure above "The Relative Strengths of Some Common Conjugate Acid–Base Pairs". The conjugate acid–base pairs are listed in order (from top to bottom) of increasing acid strength, which corresponds to decreasing values of pK_a. This order corresponds to decreasing strength of the conjugate base or increasing values of pK_b. At the bottom left of the figure  are the common strong acids; at the top right are the most common strong bases. Notice the inverse relationship between the strength of the parent acid and the strength of the conjugate base. Thus the conjugate base of a strong acid is a very weak base, and the conjugate base of a very weak acid is a strong base.

Note the Pattern

The conjugate base of a strong acid is a weak base and vice versa.

We can use the relative strengths of acids and bases to predict the direction of an acid–base reaction by following a single rule: an acid–base equilibrium always favors the side with the weaker acid and base, as indicated by these arrows:

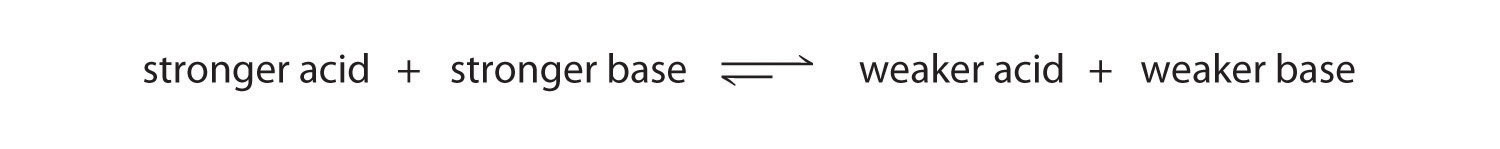
In an acid–base reaction, the proton always reacts with the stronger base.

For example, hydrochloric acid is a strong acid that ionizes essentially completely in dilute aqueous solution to produce H₃O⁺ and Cl^-; only negligible amounts of HCl molecules remain undissociated. Hence the ionization equilibrium lies virtually all the way to the right, as represented by a single arrow:

Equation 16.30

HCl (aq) + H₂O (l) --> H₃O⁺ (aq) + Cl^- (aq)

In contrast, acetic acid is a weak acid, and water is a weak base. Consequently, aqueous solutions of acetic acid contain mostly acetic acid molecules in equilibrium with a small concentration of H₃O⁺ and acetate ions, and the ionization equilibrium lies far to the left, as represented by these arrows:

Figure 16.3

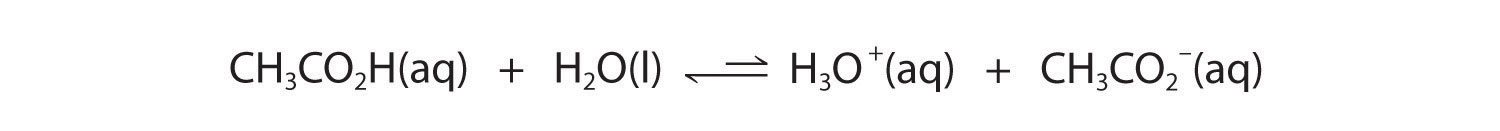
Similarly, in the reaction of ammonia with water, the hydroxide ion is a strong base, and ammonia is a weak base, whereas the ammonium ion is a stronger acid than water. Hence this equilibrium also lies to the left:

Figure 16.4

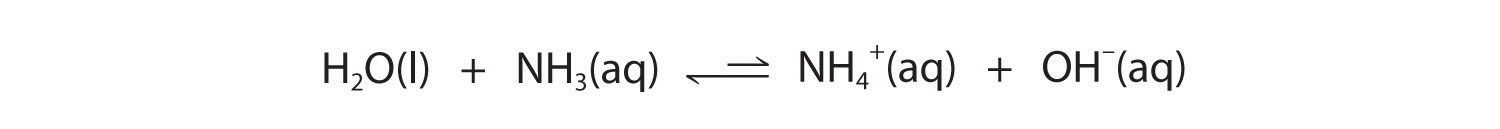
Note the Pattern

All acid–base equilibriums favor the side with the weaker acid and base. Thus the proton is bound to the stronger base.

Example 4

1. Calculate K_b and pK_b of the butyrate ion (CH₃CH₂CH₂CO₂^-). The pK_a of butyric acid at 25°C is 4.83. Butyric acid is responsible for the foul smell of rancid butter.
2. Calculate K_a and pK_a of the dimethylammonium ion [(CH₃)₂NH₂⁺]. The base ionization constant K_b of dimethylamine [(CH₃)₂NH] is 5.4 × 10^-4 at 25°C.

Worked Problem Here

Subpages (1): Example 4