A buffer is a solution that can resist pH change upon the addition of an acidic or basic components. It is able to neutralize small amounts of added acid or base, thus maintaining the pH of the solution relatively stable. This is important for processes and/or reactions which require specific and stable pH ranges. Buffer solutions have a working pH range and capacity which dictate how much acid/base can be neutralized before pH changes, and the amount by which it will change.

What is a buffer composed of?

To effectively maintain a pH range, a buffer must consist of a weak conjugate acid-base pair, meaning either a. a weak acid and its conjugate base, or b. a weak base and its conjugate acid. The use of one or the other will simply depend upon the desired pH when preparing the buffer. For example, the following could function as buffers when together in solution:

• Acetic acid (weak organic acid w/ formula CH₃COOH) and a salt containing its conjugate base, the acetate anion (CH₃COO^-), such as sodium acetate (CH₃COONa)
• Pyridine (weak base w/ formula C₅H₅N) and a salt containing its conjugate acid, the pyridinium cation (C₅H₅NH⁺), such as Pyridinium Chloride.
• Ammonia (weak base w/ formula NH₃) and a salt containing its conjugate acid, the ammonium cation, such as Ammonium Hydroxide (NH₄OH)

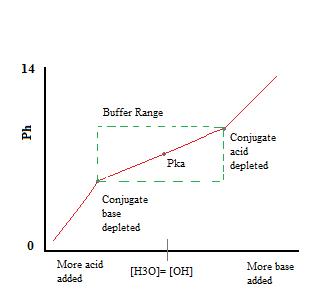
How does a buffer work?

A buffer is able to resist pH change because the two components (conjugate acid and conjugate base) are both present in appreciable amounts at equilibrium and are able to neutralize small amounts of other acids and bases (in the form of H₃O⁺ and OH^-) when the are added to the solution.

In order to clarify this effect, we can consider the simple example of a Hydrofluoric Acid (HF) and Sodium Fluoride (NaF) buffer. Hydrofluoric acid is a weak acid due to the strong attraction between the relatively small F^- ion and solvated protons (H₃O⁺), which does not allow it to dissociate completely in water. Therefore, if we obtain HF in an aqueous solution, we establish the following equilibrium with only slight dissociation (K_a(HF) = 6.6x10^-4, strongly favors reactants):

HF(aq)+H2O(l) ?F?(aq)+H3O+(aq)We can then add and dissolve sodium fluoride into the solution and mix the two until we reach the desired volume and pH at which we want to buffer.

When Sodium Fluoride dissolves in water, the reaction goes to completion, thus we obtain:

NaF(aq)+H2O(l) ?Na+(aq)+F?(aq)Since Na⁺ is the conjugate of a strong base, it will have no effect on the pH or reactivity of the buffer. The addition of NaF to the solution will, however, increase the concentration of F^- in the buffer solution, and, consequently, by Le Chatlier's principle, lead to slightly less dissociation of the HF in the previous equilibrium, as well.  The presence of significant amounts of both the conjugate acid, HF, and the conjugate base, F^-, allows the solution to function as a buffer.

This buffering action can be seen in the titration curve of a buffer solution.

As we can see, over the working range of the buffer. pH changes very little with the addition of acid or base. Once the buffering capacity is exceeded the rate of pH change quickly jumps. This occurs because the conjugate acid or base has been depleted through neutralization. This principle implies that a larger amount of conjugate acid or base will have a greater buffering capacity.

If acid is added:

F?(aq)+H3O+(aq) ? HF(aq)+H2O(l)In this reaction, the conjugate base, F^-, will neutralize the added acid, H₃O⁺, and this reaction goes to completion, because the reaction of F^- with H₃O⁺ has an equilibrium constant much greater than one.  (In fact, the equilibrium constant the reaction as written is just the inverse of the K_a for HF: 1/K_a(HF) = 1/(6.6x10^-4) = 1.5x10⁺³.)  So long as there is more F^- than H₃O⁺, almost all of the H₃O⁺ will be consumed and the equilibrium will shift to the right, slightly increasing the concentration of HF and slightly decreasing the concentration of F^-, but resulting in hardly any change in the amount of H₃O⁺ present once equilibrium is re-established. 

If base is added:

HF(aq)+OH?(aq) ? F?(aq)+H2O(l)In this reaction, the conjugate acid, HF, will neutralize added amounts of base, OH^-, and the equilibrium will again shift to the right, slightly increasing the concentration of F^- in the solution and decreasing the amount of HF slightly. Again, since most of the OH^- is neutralized, little pH change will occur.

These two reactions can continue to alternate back and forth with little pH change.

Selecting proper components for desired pH

Buffers function best when the pK_a of the conjugate weak acid used is close to the desired working range of the buffer. This turns out to be the case when the concentrations of the conjugate acid and conjugate base are approximately equal (within about a factor of 10). For example, we know the K_a for hydroflouric acid is 6.6 x 10^-4 so its pK_a= -log(6.6 x 10^-4) = 3.18. So, a hydrofluoric acid buffer would work best in a buffer range of around pH = 3.18.

For the weak base ammonia (NH₃), the value of K_b is 1.8x10^-5, implying that the K_a for the dissociation of its conjugate acid, NH₄⁺, is K_w/K_b=10^-14/1.8x10^-5 = 5.6x10^-10.  Thus, the pK_a for NH₄⁺ = 9.25, so buffers using NH₄⁺/NH₃ will work best around a pH of 9.25. (It's always the pK_a of the conjugate acid that determines the approximate pH for a buffer system, though this is dependent on the pK_b of the conjugate base, obviously.)

When the desired pH of a buffer solution is near the pK_a of the conjugate acid being used (i.e., when the amounts of conjugate acid and conjugate base in solution are within about a factor of 10 of each other), the Henderson-Hasselbalch equation can be applied as a simple approximation of the solution pH, as we will see in the next section.

Example: HF Buffer

In this example we will continue to use the hydrofluoric acid buffer. We will discuss the process for preparing a buffer of HF at a pH of 3.0. We can use the Henderson-Hasselbalch equation to calculate the necessary ratio of F-and HF. This is simply the ratio of the concentrations of conjugate base and conjugate acid we will need in our solution. However, what if we have 100 ml of 1 M HF and we want to prepare a buffer using NaF? How much Sodium Fluoride would we need to add in order to create a buffer at said pH (3.0)? We know from our Henderson-Hasselbalch calculation that the ratio of our base/acid should be equal to 0.66.  From a table of molar masses, such as a periodic table, we can calculate the molar mass of NaF to be equal to 41.99 g/mol. HF is a weak acid with a Ka = 6.6 x 10-4 and the concentration of HF is given above as 1 M. Using this information, we can calculate the amount of F- we need to add. The dissociation reaction is: HF(aq)+H2O(l) ?F?(aq)+H3O+(aq)We could use ICE tables to calculate the concentration of F- from HF dissociation, but, since Ka is so small, we can approximate that virtually all of the HF will remain undissociated, so the amount of F- in the solution from HF dissociation will be negligible.  Thus, the [HF] is about 1 M and the [F-] is close to 0.  This will be especially true once we have added more F-, the addition of which will even further suppress the dissociation of HF.  We want the ratio of Base/Acid to be 0.66, so we will need [Base]/1M = 0.66.  Thus, [F-] should be about 0.66 M.  For 100 mL of solution, then, we will want to add 0.066 moles (0.1 L x 0.66 M) of F-.  Since we are adding NaF as our source of F-, and since NaF completely dissociates in water, we need 0.066 moles of NaF.  Thus, 0.066 moles x 41.99 g/mol = 2.767 g. Note that, since the conjugate acid and the conjugate base are both mixed into the same volume of solution in the buffer, the ratio of "Base/Acid" is the same whether we use a ratio of the "concentration of base over concentration of acid," OR a ratio of "moles of base over moles of acid."  The pH of the solution does not, it turns out, depend on the volume!  (This is only true so long as the solution does not get so dilute that the autoionization of water becomes an important source of H+ or OH-.  Such dilute solutions are rarely used as buffers, however.)

Adding Strong Acids or Bases to Buffer Solutions

Now that we have this nice F^-/HF buffer, let's see what happens when we add strong acid or base to it. Recall that the amount of F^- in the solution is 0.66M x 0.1 L = 0.066 moles and the amount of HF is 1.0 M x 0.1L = 0.10 moles. Let's double check the pH using the Henderson-Hasselbalch Approximation, but using moles instead of concentrations:

pH = pK_a + log(Base/Acid) = 3.18 + log(0.066 moles F^-/0.10 moles HF) = 3.00

Good.  Now let's see what happens when we add a small amount of strong acid, such as HCl. When we put HCl into water, it completely dissociates into H₃O⁺ and Cl^-.  The Cl^- is the conjugate base of a strong acid so is inert and doesn't affect pH, and we can just ignore it. However, the H₃O⁺ can affect pH and it can also react with our buffer components. In fact, we already discussed what happens. The equation is:

F?(aq)+H3O+(aq) ? HF(aq)+H2O(l)For every mole of H₃O⁺ added, an equivalent amount of the conjugate base (in this case, F^-) will also react, and the equilibrium constant for the reaction is large, so the reaction will continue until one or the other is essentially used up. If the F^- is used up before reacting away all of the H₃O⁺, then the remaining H₃O⁺ will affect the pH directly. In this case, the capacity of the buffer will have been exceeded - a situation one tries to avoid. However, for our example, let's say that the amount of added H₃O⁺ is smaller than the amount of F^- present, so our buffer capacity is NOT exceeded.  For the purposes of this example, we'll let the added H₃O⁺ be equal to 0.01 moles (from 0.01 moles of HCl). Now, if we add 0.01 moles of HCl to 100 mL of pure water, we would expect the pH of the resulting solution to be 1.00 (0.01 moles/0.10 L = 0.1 M; pH = -log(0.1) = 1.0). 

However, we are adding the H₃O⁺ to a solution that has F^- in it, so the H₃O⁺ will all be consumed by reaction with F^-. In the process, the 0.066 moles of F^- is reduced:

0.066 initial moles F^- - 0.010 moles reacted with H₃O⁺ = 0.056 moles F^- remaining

Also during this process, more HF is formed by the reaction:

0.10 initial moles HF + 0.010 moles from reaction of F^- with H₃O⁺ = 0.11 moles HF after reaction

Plugging these new values into Henderson-Hasselbalch gives:

pH = pK_a + log (base/acid) = 3.18 + log (0.056 moles F^-/0.11 moles HF) = 2.89

Thus, our buffer did what it should - it resisted the change in pH, dropping only from 3.00 to 2.89 with the addition of 0.01 moles of strong acid.

Example 2

What is the pH of a solution that contains

1. 0.135 M HCO₂H and 0.215 M HCO₂Na? (The pK_a of formic acid is 3.75.)
2. 0.0135 M HCO₂H and 0.0215 M HCO₂Na?
3. 0.119 M pyridine and 0.234 M pyridine hydrochloride? (The pK_b of pyridine is 8.77.)

Worked Problem Here

Example 3

The buffer solution in Example 15 contained 0.135 M HCO₂H and 0.215 M HCO₂Na and had a pH of 3.95.

1. What is the final pH if 5.00 mL of 1.00 M HCl are added to 100 mL of this solution?

Worked Problem Here