Answers to Ch 18 End-of-Chapter Problems
| 1. Strategy: Write a balanced equilibrium equation for the ionization equilibrium of formic acid. Tabulate the initial concentrations, the changes, and the final concentrations.
Solution: Because sodium formate is a strong electrolyte, it ionizes completely in solution to give formate and sodium ions. The Na+ ions are spectator ions, so they can be ignored in the equilibrium equation. Because water is both a much weaker acid than formic acid and a much weaker base than formate, the acid–base properties of the solution are determined solely by the formic acid ionization equilibrium: HCO2H(aq) ? HCO2-(aq) + H+(aq) The initial concentrations, the changes in concentration that occur as equilibrium is reached, and the final concentrations can be tabulated.
We substitute the expressions for the final concentrations into the equilibrium constant expression and make our usual simplifying assumptions, so Ka=[H+][HCO2?]/[HCO2H]=(x)(0.100+x)/0.150?x=1.8×10?4Rearranging and solving for x, x=(1.8×10?4)×0.150 M0.100 M=2.7×10?4=[H+]The value of x is small compared with 0.150 or 0.100 M, so our assumption about the extent of ionization is justified. The final pH is ?log(2.7 × 10?4) = 3.57, compared with the initial value of 2.29. Thus adding a salt containing the conjugate base of the acid has increased the pH of the solution, as we expect based on Le Châtelier’s principle; the stress on the system has been relieved by the consumption of H+ ions, driving the equilibrium to the left. 2.Given: composition and pH of buffer; concentration and volume of added acid or base Asked for: final pH Strategy: A Calculate the amounts of formic acid and formate present in the buffer solution. Then calculate the amount of acid or base added. B Construct a table showing the amounts of all species after the neutralization reaction. Use the final volume of the solution to calculate the concentrations of all species. Finally, substitute the appropriate values into the Henderson-Hasselbalch equation to obtain the pH. Solution: The added HCl (a strong acid) or NaOH (a strong base) will react completely with formate (a weak base) or formic acid (a weak acid), respectively, to give formic acid or formate and water. We must therefore calculate the amounts of formic acid and formate present after the neutralization reaction. A) We begin by calculating the millimoles of formic acid and formate present in 100 mL of the initial pH 3.95 buffer. Next, we construct a table of initial amounts, changes in amounts, and final amounts:
The final amount of H+ in solution is given as “?0 mmol.” For the purposes of the stoichiometry calculation, this is essentially true, but remember that the point of the problem is to calculate the final [H+] and thus the pH. We now have all the information we need to calculate the pH. We can use either the lengthy procedure of Example 14 or the Henderson–Hasselbach equation. Because we have performed many equilibrium calculations in this chapter, we’ll take the latter approach. The Henderson-Hasselbalch equation requires the concentrations of HCO2? and HCO2H, which can be calculated using the number of millimoles (n) of each and the total volume (VT). Substituting these values into the Henderson-Hasselbalch equation, pH=pKa+log([HCO2?][HCO2H])Because the total volume appears in both the numerator and denominator, it cancels. We therefore need to use only the ratio of the number of millimoles of the conjugate base to the number of millimoles of the weak acid. So pH=pKa+log([HCO2?][HCO2H])=3.70Once again, this result makes sense on two levels. First, the addition of HCl has decreased the pH from 3.95, as expected. Second, the ratio of HCO2? to HCO2H is slightly less than 1, so the pH should be between the pKa and pKa ? 1.
B) The procedure for solving this part of the problem is exactly the same as that used in part (a). We have already calculated the numbers of millimoles of formic acid and formate in 100 mL of the initial pH 3.95 buffer: 13.5 mmol of HCO2H and 21.5 mmol of HCO2?. The number of millimoles of OH? in 5.00 mL of 1.00 M NaOH. With this information, we can construct a table of initial amounts, changes in amounts, and final amounts.
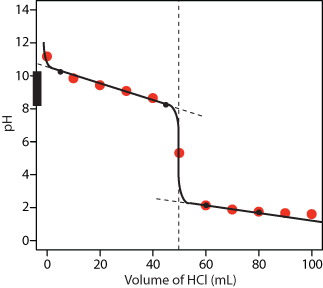
The final amount of OH? in solution is not actually zero; this is only approximately true based on the stoichiometric calculation. We can calculate the final pH by inserting the numbers of millimoles of both HCO2? and HCO2H into the simplified Henderson-Hasselbalch expression used in part (a) because the volume cancels: pH=pKa+log([HCO2?][HCO2H])=4.24Once again, this result makes chemical sense: the pH has increased, as would be expected after adding a strong base, and the final pH is between the pKa and pKa + 1, as expected for a solution with a HCO2?/HCO2H ratio between 1 and 10. 3. Follow the procedure in questions 1 and 2. Answer: 5.30 4.42 4. (a) 5. (e) 6. YouTube Video7. YouTube Video8. SOLUTION The equivalence point occurs when equal moles of acid react with equal moles of base. The mmol CH3COOH: 15mLCH3COOH?.15mmolCH3COOH1mL=2.25mmolCH3COOH We must find the amount of of mL of NaOH to give us the same mmols as CH3COOH 2.25mmolCH3COOH=0.1MNaOH?XmLNaOH X=22.5 mL Therefore the equivalence point is after the addition of 22.5 mL of NaOH 9. The two points before the equivalence point (VHCl = 5 mL, pH = 10.24 and VHCl = 45 mL, pH = 8.24) are plotted using the pKa of 9.244 for NH4+. The two points after the equivalence point (VHCl = 60 mL, pH = 2.13 and VHCl = 80 mL, pH = 1.75 ) are plotted as well.
Figure Titration curve for Practice Exercise 9.3. The black dots and curve are the approximate sketch of the titration curve. 13.
14.
15.
16. 11.6 17. 9.23 18. 43 mL 19. pH at equivalence point = 8.28
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
