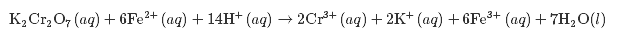HCl + NaOH à NaCl + H₂O

moles HCl = moles NaOH

Ma×Va=Mb×Vb

where the subscript ‘a’ indicates the acid, HCl, and the subscript ‘b’ indicates the base, NaOH. The volume of NaOH needed to reach the equivalence point is

Veq=Vb=Ma?Va?Mb=(0.100 M)(50.0 mL)(0.200 M)=25.0 mL NaOH

5.

6.
7.
Step 1:Split into two half reaction equations: Oxidation and ReductionOxidation: SO₃^2- (aq) ? SO₄^2- (aq)  [ oxidation because oxidation state of sulfur increase from +4 to +6]>THESE ARE THE SKELETAL HALF EQUATIONSReduction: MnO₄⁺ (aq) ? Mn²⁺ (aq) [ Reduction because oxidation state of Mn decreases from +7 to +2]Step 2:Balance each of the half equations in this order:-          Atoms other than H and O-          O atoms by adding H₂Os with proper coefficient-          H atoms by adding H⁺ with proper coefficientThe Sulfur atoms and Mn atoms are already balanced, hence we can go onto balancing O atomsOxidation: SO₃^2- (aq) + H₂O (l) ? SO₄^- (aq)Reduction: MnO₄^- (aq) ? Mn²⁺ (aq) + 4H₂O (l)Then balance out H atoms on each sideOxidation: SO₃^2- (aq) + 4H₂O (l) ? SO₄^2- (aq) + 2H⁺ (aq)Reduction: MnO₄^- (aq) + 8H⁺ (aq) ? Mn²⁺ (aq) + 4H₂O (l)Step 3:Balance the charges of the half reactions by adding electronsOxidation: SO₃^2- (aq) + H₂O (l) ? SO₄^- (aq) + 2H⁺  (aq) + 2e^-Reduction: MnO₄^- (aq) + 8H⁺ + 5e^- ? Mn²⁺ (aq) + 4H₂O (l)Step 4:Obtain the overall redox equation by combining the half reaction, but multiply entire equation by number of electrons in oxidation with reduction equation, and number of electrons in reduction with oxidation equation.Oxidation:[ SO₃^2- (aq) + H₂O (l) ? SO₄^- (aq) + 2H⁺  (aq) + 2e^-] x 5Reduction: [ MnO₄^- (aq) + 8H⁺ + 5e^-? Mn²⁺ (aq) + 4H₂O (l) ] x 2Overall Reaction:Oxidation: 5 SO₃^2- (aq) + 5H₂O (l) ? 5SO₄^2- (aq) + 10H⁺ (aq) + 10e^-+Reduction: 2 MnO₄^- (aq) + 16H⁺ (aq) +10e^- ? 2 Mn²⁺ (aq) + 8H₂O (l)5 SO₃^2- (aq) + 5H₂O (l) + 2 MnO₄^- (aq) + 16H⁺ (aq) +10e^- ? 5SO₄^2- (aq) + 10H⁺ (aq) + 10e^- +2 Mn²⁺ (aq) + 8H₂O (l)Step 5:Simplify. You can cancel out similar terms on both sides, like the 10e^- and waters.5 SO₃^2- (aq) + 2 MnO₄^- (aq) + 6H⁺ (aq)  ? 5SO₄^2- (aq) + 2Mn²⁺ (aq) + 3H₂O (l)

8. First, they are separated into the half-equations: 

MnO₄^-(aq) --> MnO₂(s) (the reduction, because oxygen is LOST) and

SO₃^2-(aq) --> SO₄^2-(aq) (the oxidation, because oxygen is GAINED)

Now, to balance the oxygen atoms, we must add two water molecules to the right side of the first equation, and one water molecule to the left side of the second equation:

MnO₄^-(aq) --> MnO₂(s) + 2H₂O(l)

H₂O(l) + SO₃^2-(aq) --> SO₄^2-(aq)

To balance the hydrogen atoms (those the original equation as well as those added in the last step), we must add four H⁺ ions to the left side of the first equation, and two H⁺ ions to the right side of the second equation.

4H⁺ + MnO₄^-(aq) --> MnO₂(s) + 2H₂O(l)

H₂O(l) + SO₃^2-(aq) --> SO₄^2-(aq) + 2H⁺

Now we must balance the charges. In the first equation, the charge is +3 on the left and 0 on the right, so we must add three electrons to the left side to make the charges the same. In the second equation, the charge is -2 on the left and 0 on the right, so we must add two electrons to the right.

3e^- + 4H⁺ + MnO₄^-(aq) --> MnO₂(s) + 2H₂O(l)

H₂O(l) + SO₃^2-(aq) --> SO₄^2-(aq) + 2H⁺ + 2e^-

Now we must make the electrons equal eachother, so we multiply each equation by the appropriate number to get the common multiple (in this case, by 2 for the first equation, and by 3 for the second).

2(3e^- + 4H⁺ + MnO₄^-(aq) --> MnO₂(s) + 2H₂O(l))

3(H₂O(l) + SO₃^2-(aq) --> SO₄^2-(aq) + 2H⁺ + 2e^-)

With the result:

6e^- + 8H⁺ + 2MnO₄^-(aq) --> 2MnO₂(s) + 4H₂O(l)

3H₂O(l) + 3SO₃^2-(aq) --> 3SO₄^2-(aq) + 6H⁺ + 6e^-

Now we cancel and add the equations together. We can cancel the 6e^- because they are on both sides. We can get rid of the 6H⁺ on both sides as well, turning the 8H⁺ in the first equation to 2H⁺. The same method gets rid of the 3H₂O(l) on the bottom, leaving us with just one H₂O(l) on the top. In the end, the overall reaction should have no electrons remaining. Now we can write one balanced equation:

2MnO₄^-(aq) + 2H⁺ + 3SO₃^2-(aq) --> H₂O(l) + 2MnO₂(s) + 3SO₄^2-(aq)

The equation is now balanced in an acidic environment. If necessary, we can balance in a basic environment by adding OH^- to turn the H⁺ into water molecules as follows:

 2MnO₄^-(aq) + H₂O + 3SO₃^2-(aq) --> H₂O(l) + 2MnO₂(s) + 3SO₄^2-(aq) + 2OH^-

The equation is now balanced in a basic environment.

9. 

Step 1:Reduction: OCl^-  ? Cl^-Oxidation:   Fe(OH)₃ ? FeO₄^2-Step 2/3:Reduction:  2H⁺ +  OCl^- + 2e^- ? Cl^- + H₂OOxidation:  Fe(OH)₃ + H₂O  ? FeO₄^2- + 3e^- + 5H⁺Step 4:Overall Equation:[ 2H⁺ +  OCl^- + 2e^- ? Cl^- + H₂O ] x 3[ Fe(OH)₃ + H₂O  ? FeO₄^2- + 3e^- + 5H⁺ ] x 2=6H⁺ + 3OCl^- + 6e^- ? 3Cl^- +3 H₂O+2Fe(OH)₃ +2 H₂O  ? 2FeO₄^2- + 6e^- + 10H⁺6H⁺ + 3OCl^- + 2e^- + 2Fe(OH)₃ +2 H₂O  ? 3Cl^- +3 H₂O + 2FeO₄^2- + 6e^- + 10H⁺ Step 5:Simplify: 3OCl^- + 2Fe(OH)₃  ? 3Cl^- + H₂O + 2FeO₄^2- + 4H⁺
10.
Step 1:Oxidation:    Fe²⁺ ? Fe³⁺Reduction:   VO₄^3- ? VO²⁺ Step 2/3:Oxidation: Fe²⁺ ? Fe³⁺ + e^-Reduction: 6H⁺ + VO₄^3- + e^- ? VO²⁺ + 3H₂OStep 4:Overall Reaction:Fe²⁺ ? Fe³⁺ + e^-+6H⁺ + VO₄^3- + e^-? VO²⁺ + 3H₂O____________________________ Fe²⁺ +  6H⁺ + VO₄^3- + e^- ? Fe³⁺ + e^- + VO²⁺ + 3H₂OStep 5:Simplify:Fe²⁺ +  6H⁺ + VO₄^3-  ? Fe³⁺  + VO²⁺ + 3H₂O
11.
12.a)