`I = (( "b" * "h" ^3)/12)"," (( "b" ^3* "h" )/4)`

Enter a value for all fields

This equation computes the Area Moment of Inertia for a right triangle with right angle on right of the base. The putput of this equation ios the `I_x` and `I_y` component of the area moment of inertia when the triangle is defined to be in the x/y plane

The Area Moment of Inertia (I), also called the second moment of area, polar moment of inertia or second area moment, represents how area is distributed around the center of mass. The Area Moment of Inertia has units of length to the fourth power.

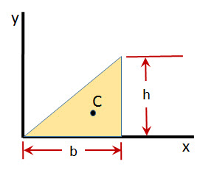
/attachments/5727d26f-78cc-11e5-a3bb-bc764e2038f2/AreaMomentofInertiaTriangleRtAngleRight-illustration.png

Reference

Fundamentals of Engineering. 8th edition, 2nd Revision. National Council of Examiners for Engineering and Surveying (NCEES) - 2001. ISBN 978-1-932613-59-9. pg51