Angular Frequency of Physical Pendulum

Processing...

The Angular Frequency of a Physical Pendulum calculator computes the approximate value of the angular frequency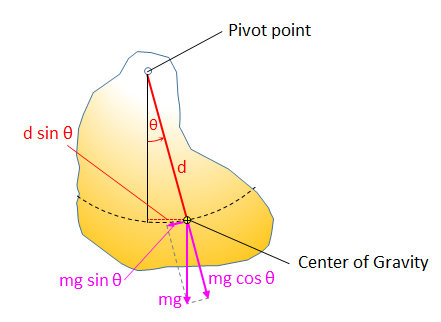 given that the amplitude of the pendulum is small based on the mass, distance from pivot point to center of mass and the moment of inertia.

INSTRUCTIONS: Choose units and enter the following:

(m) Mass of Pendulum
(d) Distance from Pivot Point to Center of Gravity
(I) Moment of Inertia

Angular Frequency(ω): The calculator returns the angular frequency in units radians per minute.

The Math / Science

The formula used in this calculator is as follows:

`omega = sqrt((m*g*d)/I)`

A physical pendulum is a body or mass suspended from a rotation point as shown in the figure. The gravitational force acts on the body at the center of gravity. This formula employs the acceleration due to gravity at sea-level on Earth (g = 9.80665 m/s²)

Envision how the two component forces change as the pendulum swings. The force of gravity `m*g` remains constant, while the force acting to return the body to equilibrium, `m*g*sin(theta)`, increases to it's maximum value (equal to `m*g`) at `theta` = 90^o.

Moment of Inertia

vCalc has many formulas to compute the Moment of Inertia of different shapes. The Moment of Inertia library can be found HERE. A calculator with many of the MOI equations can be found HERE.

A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force combined with the pendulum's mass causes it to oscillate about the equilibrium position, swinging back and forth. The time for one complete cycle, a left swing and a right swing, is called the period. The period depends on the length of the pendulum, and also to a slight degree on the amplitude, the width of the pendulum's swing.

Types of Pendulums:

Simple Pendulum – A single mass (bob) attached to a string or rod that swings back and forth.
Compound Pendulum – A rigid body swinging about a pivot point.
Foucault Pendulum – Demonstrates the Earth's rotation by slowly changing its plane of motion.
Torsional Pendulum – Rotates around its axis instead of swinging back and forth.

Applications of Pendulums:

Used in clocks (grandfather clocks) to regulate time.
Scientific experiments (measuring gravity).
Seismometers to detect earthquakes.
Amusement park rides.

The Pendulum Calculator includes the basic physics formulas and constants for the properties of a pendulum. These include the following:

Pendulum Frequency: Computes the frequency (ƒ) of a simple pendulum based on the length (L) of the pendulum.
Period of a Pendulum: Computes the period (T) of a simple pendulum based on the length (L) of the pendulum arm and the acceleration due to gravity (g).
Pendulum Length: Computes the length (L) of a simple pendulum based on the period (T) of the pendulum arm and the acceleration due to gravity (g).
Pendulum Angular Frequency: Computes the angular frequency of a simple pendulum with a small amplitude.
Angular Frequency of a Physical Pendulum: Computes the approximate value of the angular frequency given that the amplitude of the pendulum is small based on the mass, distance from pivot point to center of mass and the moment of inertia.
Restoring Torque to a Pendulum: Computes the restoring torque (τz) on a physical pendulum based on the mass (m), acceleration due to gravity (g), distance to the center of gravity (d) and the displacement angle (θ).
Restoring Force on a Pendulum: Approximates the restoring force on a pendulum based on the mass, length of pendulum and length of arc.
Rotational Acceleration of a Physical Pendulum: Approximates the rotational acceleration of a physical pendulum based on the mass (m), acceleration due to gravity (g), distance to the center of gravity (d), impulse (I) and the angle (Θ)
(g) acceleration due to gravity

Reference

Young, Hugh and Freeman, Roger. University Physics With Modern Physics. Addison-Wesley, 2008. 12th Edition, (ISBN-13: 978-0321500625 ISBN-10: 0321500628 ) Pg 438, eq 13.38