From UCDavis Chemwiki

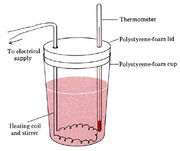
Figure 2 A coffee-cup
calorimeter.
In an elementary laboratory, enthalpy changes are often measured in a “coffee-cup calorimeter” such as that shown in Fig. 15.1.2. Suppose the reaction to be measured is between two solutions. One of these solutions is introduced into the coffee cup, and the temperature of both solutions is measured.

The second solution is now introduced, the mixture stirred, and the rise in temperature recorded. Since the cup is made of polystyrene foam, a very good insulator, very little heat energy escapes. It may be measurable, however, and may be represented by the calorimeter constant.

Calorimeter Constant

A simple experiment can be used to determine how much energy is lost to the calorimeter, the thermometer, and the surroundings. This energy loss, divided by the temperature change in the calorimeter that caused it, is often called the "calorimeter heat capacity" or "calorimeter constant" as illustrated by the following example:

Using the Calorimeter Constant

The heat absorbed by the calorimeter and its contents is equal to the heat released by a chemical reaction, as illustrated by the following example:

Example 3: The calorimeter above contains 250.0 cm³ of 1.000 M HCl (D = 1.02 g/cm³) at 20.38°C and to this is added, with stirring, 250.0 cm³ of 1.000 M NaOH (D = 1.04 g/cm³) also at 20.38°C. The temperature of the mixture rises to 27.80°C. Assuming that the specific heat capacity of the NaCl solution that results is 4.20J/g°C, calculate `DeltaH`, for the reaction

`H_3O^(+)(aq) + OH^(-)(aq) -> 2H<sub>2</sub>O(l)`

Solution:

To calculate `DeltaH`, we need to divide the enthalpy change by the amount of product, in moles. Since 250 mL of 1 M solutions of each reactant are mixed and they are in a 1:1 stoichiometric ratio, we will produce 0.250 mol (n = C × V mol = 0.250 L x 1.00 mol/L) of product, so:

`DeltaH = (-16.2 kJ)/(0.250 mol) = 64.7 kJ" " mol^(-1)`