Colligative Properties and Dissociation of Electrolytes

Thus far we have assumed that we could simply multiply the molar concentration of a solute by the number of ions per formula unit to obtain the actual concentration of dissolved particles in an electrolyte solution. For example if we have a 2.0 M solution of NaCl we assume that in 1 liter of this solution, we would have 2 moles of Na⁺ and 2 moles of Cl^-.

We have used this simple model to predict such properties as freezing points, melting points, vapor pressure, and osmotic pressure. If this model were perfectly correct, we would expect the freezing point depression of a 0.10 m solution of sodium chloride, with 2 mol of ions per mole of NaCl in solution, to be exactly twice that of a 0.10 m solution of glucose, with only 1 mol of molecules per mole of glucose in solution. In reality, this is not always the case. Instead, the observed change in freezing points for 0.10 m aqueous solutions of NaCl and KCl are significantly less than expected (?0.348°C and ?0.344°C, respectively, rather than ?0.372°C), which suggests that fewer particles than we expected are present in solution.

The relationship between the actual number of moles of solute added to form a solution and the apparent number as determined by colligative properties is called the van’t Hoff factor(i)and is defined as follows:

The van't Hoff factor is the ratio between the actual concentration of particles produced when the substance is dissolved, and the concentration of a substance as calculated from its mass. The van't Hoff factor, i=apparent number of particles in solution number of moles of solute dissolved.

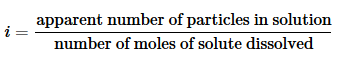
Note the Pattern

As the solute concentration increases the van’t Hoff factor decreases.

The van’t Hoff factor is therefore a measure of a deviation from ideal behavior. The lower the van’t Hoff factor, the greater the deviation. As the data in Table 14.4.1 below "van’t Hoff Factors for 0.0500 M Aqueous Solutions of Selected Compounds at 25°C" show, the van’t Hoff factors for ionic compounds are somewhat lower than expected; that is, their solutions apparently contain fewer particles than predicted by the number of ions per formula unit. As the concentration of the solute increases, the van’t Hoff factor decreases because ionic compounds generally do not totally dissociate in aqueous solution.

Table 15 Van’t Hoff Factors for 0.0500 M Aqueous Solutions of Selected Compounds at 25°C

Compound	i (measured)	i (ideal)
glucose	1.0	1.0
sucrose	1.0	1.0
`NaCl`	1.9	2.0
`HCl`	1.9	2.0
`MgCl_2`	2.7	3.0
`FeCl_3`	3.4	4.0
`Ca(NO_3)_2`	2.5	3.0
`AlCl_3`	3.2	4.0
`MgSO_4`	1.4	2.0

Instead, some of the ions exist as ion pairs, a cation and an anion that for a brief time are associated with each other without an intervening shell of water molecules (Figure 14.4.1 "Ion Pairs"). Each of these temporary units behaves like a single dissolved particle until it dissociates. Highly charged ions such as Mg²⁺, Al³⁺, SO₄^2?, and PO₄^3? have a greater tendency to form ion pairs because of their strong electrostatic interactions. The actual number of solvated ions present in a solution can be determined by measuring a colligative property at several solute concentrations.

Figure 15 Ion Pairs

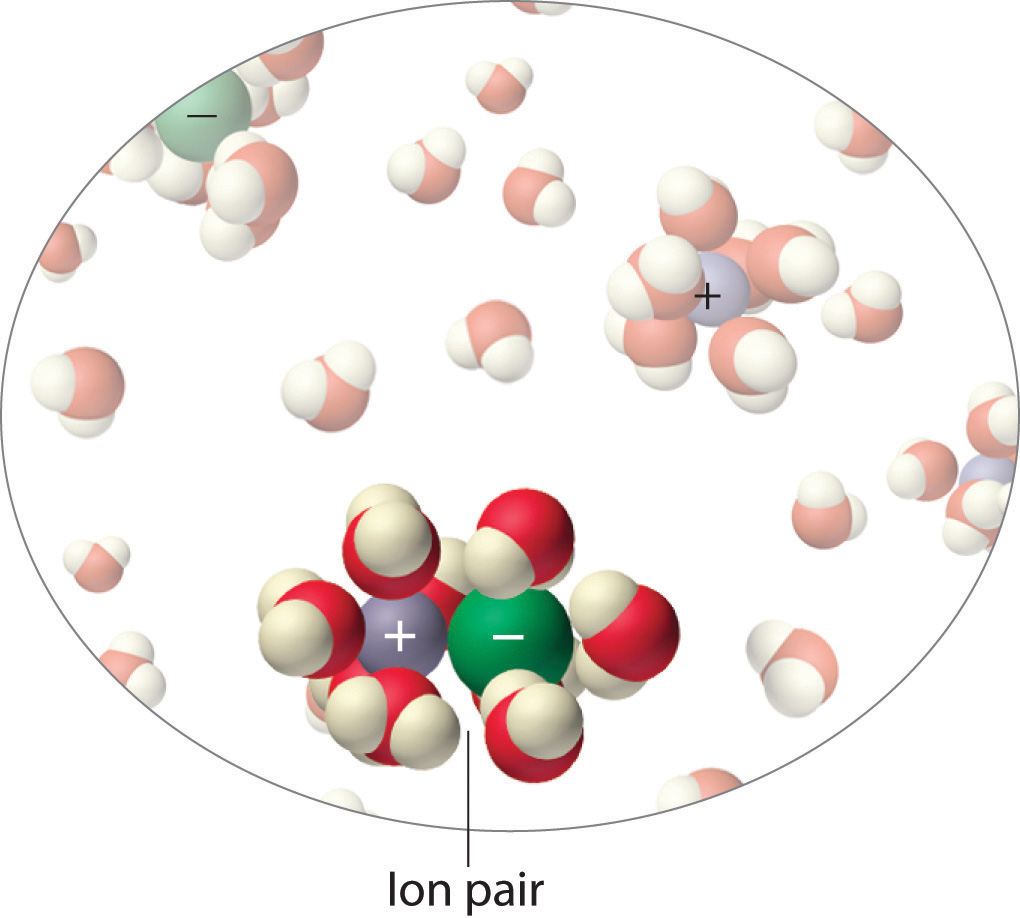
In concentrated solutions of electrolytes like NaCl, some of the ions form neutral ion pairs that are not separated by solvent and diffuse as single particles.

Example Problem 10

A 0.0500 M aqueous solution of FeCl₃ has an osmotic pressure of 4.15 atm at 25°C. Calculate the van’t Hoff factor i for the solution.

Solution:

A If `FeCl_3` dissociated completely in aqueous solution, it would produce four ions per formula unit [Fe3+(aq) plus 3Cl−(aq)] for an effective concentration of dissolved particles of `4 × 0.0500 M = 0.200 M`. The osmotic pressure would be

`Π=MRT=(0.200mol"/"L)[0.0821("L"*"atm")"/"(K*"mol")](298K)=4.89atm`

B The observed osmotic pressure is only 4.15 atm, presumably due to ion pair formation. The ratio of the observed osmotic pressure to the calculated value is 4.15 atm/4.89 atm = 0.849, which indicates that the solution contains (0.849)(4) = 3.40 particles per mole of FeCl3FeCl3 dissolved. Alternatively, we can calculate the observed particle concentration from the osmotic pressure of 4.15 atm:

`4.15atm=M[0.0821("L"*"atm")"/"("K"*"mol")](298K)`

`0.170mol"/"L=M`