Dispersal of Energy and Matter

A closer look at disorder: microstates and macrostates

How can we express disorder quantitatively? For example, let's look at the tossing of some coin. When you toss these coins and allow them to fall head or tails, you can probably see that simple statistics plays a role: the probability of obtaining three heads and seven tails after tossing ten coins is just the ratio of the number of ways that ten different coins can be arranged in this way, to the number of all possible arrangements of ten coins.

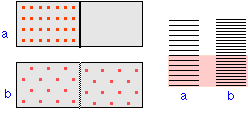
Using the language of molecular statistics, we say that a collection of coins in which a given fraction of its members are heads-up constitutes a macroscopic state of the system. Since we don’t care which coins are heads-up, there are clearly numerous configurations of the individual coins which can result in this “macrostate”. Each of these configurations specifies a microscopic state of the system.

The greater the number of microstates that correspond to a given macrostate,
the greater the probability of that macrostate.To see what this means, consider the possible outcomes of a toss of four coins:

macrostate	ways	probability	microstates
0 heads	1	1/16	TTTT
1 head	4	4/16 = 1/4	HTTT THTT TTHT TTTH
2 heads	6	6/16 = 3/8	HHTT HTHT HTTH THHT TTHH THTH
3 heads	4	4/16 = 1/4	HHHT HTHH HHTH THHH
4 heads	1	1/16	HHHH

A toss of four coins will yield one of the five outcomes (macrostates) listed in the leftmost column of the table. The second column gives the number of “ways”— that is, the number of head/tail configurations of the set of coins (the number of microstates)— that can result in the macrostate. The probability of a toss resulting in a particular macrostate is proportional to the number of microstates corresponding to the macrostate, and is equal to this number, divided by the total number of possible microstates (in this example, 2⁴ =16). An important assumption here is that all microstates are equally probable; that is, the toss is a “fair” one in which the many factors that determine the trajectory of each coin operate in an entirely random way.

Disorder is more probable than order because there are so many more ways of achieving it. Thus coins and cards tend to assume random configurations when tossed or shuffled, and socks and books tend to become more scattered about a teenager’s room during the course of daily living. But there are some important differences between these large-scale mechanical, or macro systems, and the collections of sub-microscopic particles that constitute the stuff of chemistry, and which we will refer to here generically as molecules. Molecules, unlike macro objects, are capable of accepting, storing, and giving up energy in tiny amounts (quanta), and act as highly efficient carriers and spreaders of thermal energy as they move around. Thus, in chemical systems,

1. We are dealing with huge numbers of particles. This is important because statistical predictions are always more accurate for larger samples. Thus although for the four tosses there is a good chance (62%) that the H/T ratio will fall outside the range of 0.45 - 0.55, this probability becomes almost zero for 1000 tosses. To express this in a different way, the chances that 1000 gas molecules moving about randomly in a container would at any instant be distributed in a sufficiently non-uniform manner to produce a detectable pressure difference between the two halves of a container will be extremely small. If we increase the number of molecules to a chemically significant number (around 10²⁰, say), then the same probability becomes indistinguishable from zero.
2. Once the change begins, it proceeds spontaneously. That is, no external agent (a tosser, shuffler, or teenager) is needed to keep the process going. Gases will spontaneously expand if they are allowed to, and reactions, one started, will proceed toward equilibrium.
3. Thermal energy is continually being exchanged between the particles of the system, and between the system and the surroundings. Collisions between molecules result in exchanges of momentum (and thus of kinetic energy) amongst the particles of the system, and (through collisions with the walls of a container, for example) with the surroundings.
4. Thermal energy spreads rapidly and randomly throughout the various energetically accessible microstates of the system. The direction of spontaneous change is that which results in the maximum possible spreading and sharing of thermal energy.

The importance of these last two points is far greater than you might at first think, but to fully appreciate this, you must recall the various ways in which thermal energy is stored in molecules— hence the following brief review.

From coins to molecules: the spreading of energy

Thermal energy is the portion of a molecule's energy that is proportional to its temperature, and thus relates to motion at the molecular scale. What kinds of molecular motions are possible? For monatomic molecules, there is only one: actual movement from one location to another, which we call translation. Since there are three directions in space, all molecules possess three modes of translational motion.

For polyatomic molecules, two additional kinds of motions are possible. One of these is rotation; a linear molecule such as CO₂ in which the atoms are all laid out along the x-axis can rotate along the y- and z-axes, while molecules having less symmetry can rotate about all three axes. Thus linear molecules possess two modes of rotational motion, while non-linear ones have three rotational modes.

Finally, molecules consisting of two or more atoms can undergo internal vibrations. For freely moving molecules in a gas, the number of vibrational modes or patterns depends on both the number of atoms and the shape of the molecule, and it increases rapidly as the molecule becomes more complicated.

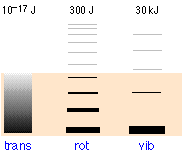
The relative populations of the translational, rotational and vibrational energy states of a typical diatomic molecule are depicted by the thickness of the lines in this schematic (not-to-scale!) diagram. The colored shading indicates the total thermal energy available at a given temperature. The numbers at the top show order-of-magnitude spacings between adjacent levels. It is readily apparent that virtually all the thermal energy resides in translational states.

Notice the greatly different spacing of the three kinds of energy levels. This is extremely important because it determines the number of energy quanta that a molecule can accept, and, as the following illustration shows, the number of different ways this energy can be distributed amongst the molecules.

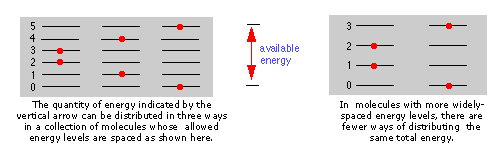
Accessible energy states. The more closely spaced the quantized energy states of a molecule, the greater will be the number of ways in which a given quantity of thermal energy can be shared amongst a collection of these molecules.

The spacing of molecular energy states becomes closer as the mass and number of bonds in the molecule increases, so we can generally say that the more complex the molecule, the greater the density of its energy states.

This is a feature of the particle-in-a-box model, which predicts that the separation of the energy states of a gas confined within a box depends on the inverse square of the box length (and on the inverse of the particle mass as well.)

3  Quantum states, microstates, and energy spreading

At the atomic and molecular level, all energy is quantized; each particle possesses discrete states of kinetic energy and is able to accept thermal energy only in packets whose values correspond to the energies of one or more of these states. Polyatomic molecules can store energy in rotational and vibrational motions, and all molecules (even monatomic ones) will possess translational kinetic energy (thermal energy) at all temperatures above absolute zero. The energy difference between adjacent translational states is so minute (roughly 10^–30 J) that translational kinetic energy can be regarded as continuous (non-quantized) for most practical purposes.

The number of ways in which thermal energy can be distributed amongst the allowed states within a collection of molecules is easily calculated from simple statistics, but we will confine ourselves to an example here. Suppose that we have a system consisting of three molecules and three quanta of energy to share among them. We can give all the kinetic energy to any one molecule, leaving the others with none, we can give two units to one molecule and one unit to another, or we can share out the energy equally and give one unit to each molecule. All told, there are ten possible ways of distributing three units of energy among three identical molecules as shown here:

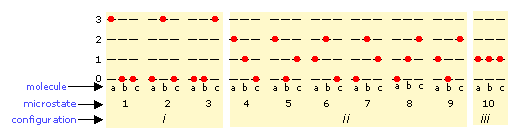
Each of these ten possibilities represents a distinct microstate that will describe the system at any instant in time. Those microstates that possess identical distributions of energy among the accessible quantum levels (and differ only in which particular molecules occupy the levels) are known as configurations. Because all microstates are equally probable, the probability of any one configuration is proportional to the number of microstates that can produce it. Thus in the system shown above, the configuration labeled ii will be observed 60% of the time, while iii will occur only 10% of the time.

huge ... Huge ... HUGE !

As the number of molecules and the number of quanta increases, the number of accessible microstates grows explosively; if 1000 quanta of energy are shared by 1000 molecules, the number of available microstates will be around 10⁶⁰⁰— a number that greatly exceeds the number of atoms in the observable universe! The number of possible configurations (as defined above) also increases, but in such a way as to greatly reduce the probability of all but the most probable configurations. Thus for a sample of a gas large enough to be observable under normal conditions, only a single configuration (energy distribution amongst the quantum states) need be considered; even the second-most-probable configuration can be neglected.

The bottom line: any collection of molecules large enough in numbers to have chemical significance will have its therrmal energy distributed over an unimaginably large number of microstates. The number of microstates increases exponentially as more energy states ("configurations" as defined above) become accessible owing to

• Addition of energy quanta (higher temperature),
• Increase in the number of molecules (resulting from dissociation, for example).
• the volume of the system increases (which decreases the spacing between energy states, allowing more of them to be populated at a given temperature.)

Why do gases tend to expand but never contract?

Everybody knows that a gas, if left to itself, will tend to expand so as to fill the volume within which it is confined completely and uniformly. What “drives” this expansion? At the simplest level it is clear that with more space available, random motions of the individual molecules will inevitably disperse them throughout the space. But as we mentioned above, the allowed energy states that molecules can occupy are spaced more closely in a larger volume than in a smaller one. The larger the volume available to the gas, the greater the number of energy states (and thus microstates) its thermal energy can occupy. Since all such microstates within the thermally accessible range of energies are equally probable, the expansion of the gas can viewed as a consequence of the tendency of energy to be spread and shared as widely as possible. Once this has happened, the probability that this sharing of energy will reverse itself (that is, that the gas will spontaneously contract) is so minute as to be unthinkable.

The same can in fact be said for even other highly probable distributions, such as having 49.999% of the molecules in the left half of the container and 50.001% in the right half. Even though the number of possible configurations that would yield this distribution of molecules is inconceivably great, it is essentially negligible compared to the number that would correspond to an exact 50-percent distribution.

The illustration represents the allowed thermal energy states of an ideal gas. The larger the volume in which the gas is confined, the more closely-spaced are these states, resulting in a huge increase in the number of microstates into which the available thermal energy can reside; this can be considered the origin of the thermodynamic "driving force" for the spontaneous expansion of a gas.

Why heat flows from hot to cold

Just as gases spontaneously change their volumes from “smaller-to-larger”, the flow of heat from a warmer body to a cooler always operates in the direction “warmer-to-cooler” because this allows thermal energy to occupy a larger number of energy states as new ones are made available by bringing the cooler body into contact with the warmer one; in effect, the thermal energy becomes more “diluted”.

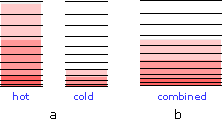
When two bodies at different temperatures are placed in thermal contact, thermal energy flow from the warmer into the cooler one until they reach the same temperature.

(a) Schematic depiction of the thermal energy states in two separated identical bodies at different temperatures (indicated by shading.)

(b) When the bodies are brought into thermal contact, thermal energy flows from the higher occupied levels in the warmer object into the unoccupied levels of the cooler one until equal numbers are occupied .

As you might expect, the increase in the amount of energy spreading and sharing is proportional to amount of heat transferred q, but there is one other factor involved, and that is the temperature at which the transfer occurs. When a quantity of heat q passes into a system at temperature T, the degree of dilution of the thermal energy is given by q /T

To understand why we have to divide by the temperature, consider the effect of very large and very small values of T in the denominator. If the body receiving the heat is initially at a very low temperature, relatively few thermal energy states are occupied, so the amount of energy spreading can be very great. Conversely, if the temperature is initially large, the number of new thermal energy states that become occupied will be negligible compared to the number already active.

The final state of a system can be more probable than its initial state (spontaneous, product-favored) in either or both of two ways:

1. Energy can be dispersed over a greater number and variety of molecules.
2. The particles of the system can be more dispersed (more disordered).