Dissolution of Solids in Liquids

From ChemPRIME

Entropy of dissolution

As anyone who has shuffled a deck of cards knows, disordered arrangements of objects are statistically more favored simply because there are more ways in which they can be realized. And as the number of objects increases, the more does statistics govern their most likely arrangements. The numbers of objects (molecules) we deal with in Chemistry is so huge that their tendency to become as spread out as possible becomes overwhelming. But in doing so, the thermal energy they carry with them is also spread and dispersed, so the availability of this energy, as measured by the temperature, is also of importance. Chemists use the term "entropy" to denote this aspect of molecular randomness.

Readers of this section who have had some exposure to thermodynamics will know that solubility, like all equilibria, is governed by the Gibbs free energy change for the process, which incorporates the entropy change at a fundamental level. This topic is treated in some detail in the unit on the Thermodynamics of Equilibrium.

A proper understanding of these considerations requires some familiarity with thermodynamics, which most students do not encounter until well into their second semester of Chemistry. For now, we will think of molecular "disorder" and entropy simply in terms of "spread-outedness".

Thus in the very common case in which a small quantity of solid or liquid dissolves in a much larger volume of solvent, the solute becomes more spread out in space, and the number of equivalent ways in which the solute can be distributed within this volume is greatly increased. This is the same as saying that the entropy of the solute increases.

If the energetics of dissolution are favorable, this increase in entropy means that the conditions for solubility will always be met. Even if the energetics are slightly endothermic the entropy effect can still allow the solution to form, although perhaps limiting the maximum concentration that can be achieved.

In such a case, we may describe the solute as being slightly soluble in a certain solvent. What this means is that a greater volume of solvent will be required to completely dissolve a given mass of solute.

"Like dissolves Like"

Chemical theory has not reached the point where it can predict exactly how much of one substance will dissolve in another. The best we can do is to indicate in general terms the relationships between solubility and the microscopic structures of solute and solvent.

To begin with, moving particles of any kind tend to become more randomly distributed as time passes. If you put a layer of red marbles in the bottom of a can and cover it with a second layer of white marbles, shaking the can for a short time will produce a nearly random distribution. The same principle applies on the microscopic level. Moving molecules tend to become randomly distributed among one another, unless something holds them back. Thus gases, whose molecules are far apart and exert negligible forces on one another, are all completely miscible with other gases.

In liquid solutions, the molecules are much closer together and the characteristics of different types of molecules are much more important. In particular, if the solute molecules exert large intermolecular forces on each other but do not attract solvent molecules strongly, the solute molecules will tend to group together. This forms a separate phase and leaves the solvent as a second phase. Conversely, if the solvent molecules attract each other strongly but have little affinity for solute molecules, solvent molecules will segregate, and two phases will form.

A classic example of the second situation described in the previous paragraph is the well-known fact that oil and water do not mix—or if they do, they do not stay mixed for long. The reason is that oil consists of alkanes and other nonpolar molecules, while water molecules are polar and can form strong hydrogen bonds with each other. Suppose that alkane or other nonpolar molecules are randomly dispersed among water molecules, as shown in part a of Figure 4.The constant jostling of both kinds of molecules will soon bring two water molecules together. Dipole forces and hydrogen bonding will tend to hold the water molecules together, but there are only weak London forces between water and nonpolar molecules. Before long, clusters of water molecules like those in part b will have formed. 

Figure 4

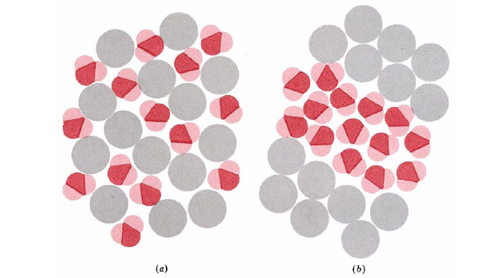
The insolubility of nonpolar molecules in water. Even if it were possible to mix nonpolar molecules (shown in gray) and water molecules as shown in (a), this situation would be unstable. The water molecules would soon congregate together under the influence of their dipole and hydrogen-bonding attractions, attaining the situation of lower energy shown in (b).

These clusters will be stable at room temperature because the energy of interaction between the water molecules will be larger than the average energy of molecular motion. Only an occasional molecular collision will be energetic enough to bump two water molecules apart, especially if they are hydrogen bonded. Given enough time, this process of aggregation will continue until the polar molecules are all collected together. If the nonpolar substance is a liquid, this process corresponds on the macroscopic level to the liquids separating from each other and forming two layers.

If instead of mixing substances like oil and water, in which there are quite different kinds of intermolecular attractions, we mix two polar substances or two nonpolar substances, there will be a much smaller tendency for one type of molecule to segregate from the other. Thus two alkanes like n-heptane, C₇H₁₆, and n-hexane, C₆H₁₄, are completely miscible in all proportions. The C₇H₁₆ and C₆H₁₄ molecules are so similar (recall the projection formulas of alkanes) that there are only negligible differences in intermolecular forces. Thus the molecules remain randomly mixed as they jostle among one another.

For a similar reason, methanol, CH₃OH, is completely miscible with water. In this case both molecules are polar and can form hydrogen bonds among themselves, and so there are strong intermolecular attractions within each liquid. However, CH₃OH dipoles can align with H₂O dipoles, and CH₃OH molecules can hydrogen bond to H₂O molecules, and so the attractions among unlike molecules in the solution are similar to those among like molecules in each pure liquid. Again there is little tendency for one type of molecule to become segregated from the other.

All the cases just discussed are examples of the general rule that like dissolves like. Two substances whose molecules have very similar structures and consequently similar intermolecular forces will usually be soluble in each other. Two substances whose molecules are quite different will not mix randomly on the microscopic level. In general, polar substances will dissolve other polar substances, while nonpolar materials will dissolve other nonpolar materials. The greater the difference in molecular structure (and hence in intermolecular attractions), the lower the mutual solubility. 

EXAMPLE 2 Predict which of the following compounds will be most soluble in water:

a)

b)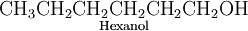

Solutions of molecular solids in liquids

The stronger intermolecular forces in solids require more input of energy in order to disperse the molecular units into a liquid solution, but there is also a considerable increase in entropy that can more than compensate if the intermolecular forces are not too strong, and if the solvent has no strong hydrogen bonds that must be broken in order to introduce the solute into the liquid.

 

solvent `=>`	non polar liquid	polar liquid
energy to disperse solute	moderate	moderate
energy to introduce into solvent	small	moderate
increase in entropy	moderate	moderate
miscibility	moderate	small

For example, at 25° C and 1 atm pressure, 20 g of iodine crystals will dissolve in 100 ml of ethyl alcohol, but the same quantity of water will dissolve only 0.30 g of iodine.

As the molecular weight of the solid increases, the intermolecular forces holding the solid together also increase, and solubilities tend to fall off; thus the solid linear hydrocarbons CH₃(CH₂)_nCH₃ (n > 20) show diminishing solubilities in hydrocarbon liquids.

Solutions of ionic solids in liquids

Since the coulombic forces that bind ions and highly polar molecules into solids are quite strong, we might expect these solids to be insoluble in just about any solvent. Ionic solids are insoluble in most non-aqueous solvents, but the high solubility of some (including NaCl) in water suggests the need for some further explanation.

solvent `=>`	non polar	polar (water)
energy to disperse solute	large	large (endothermic)
energy to introduce into liquid	small	highly negative (exothermic)
increase in entropy	moderate	moderate to slightly negative
miscibility	very small	small to large

The key factor here turns out to be the interaction of the ions with the solvent. The electrically-charged ions exert a strong coulombic attraction on the end of the water molecule that has the opposite partial charge.

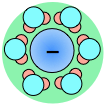
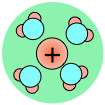
As a consequence, ions in solution are always hydrated; that is, they are quite tightly bound to water molecules through ion-dipole interaction. The number of water molecules contained in the primary hydration shell varies with the radius and charge of the ion.

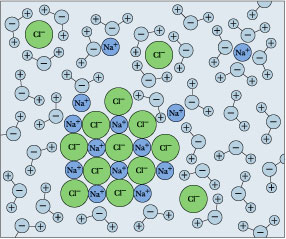
Hydration shells around some ions in a sodium chloride solution. The average time an ion spends in a shell is about 2-4 nanoseconds. But this is about two orders of magnitude longer than the lifetime of an individual H2O–H2O hydrogen bond.

 

Lattice and hydration energies

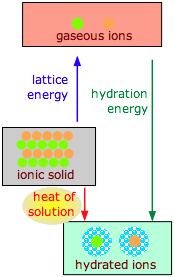
The dissolution of an ionic solid MX in water can be thought of as a sequence of two steps:

(1) MX(s) `=>` M⁺(g) + X^–(g) 

(2) M⁺(g) + X^–(g) + H₂O `=>` M⁺(aq) + X^–(aq)

• The first reaction is always endothermic; it takes a lot of work to break up an ionic crystal lattice.
• The hydration step is always exothermic as H₂O molecules are attracted into the electrostatic field of the ion.
• The heat (enthalpy) of solution is the sum of the lattice and hydration energies, and can have either sign.

Hydration Energies (`kJ mol^(-1)`)
H+(g)	–1075	F–(g)	–503
Li+(g)	–515	Cl–(g)	–369
Na+(g)	–405	Br–(g)	–336
K+(g)	–321	I–(g)	–398
Mg2+(g)	–1922	OH–(g)	–460
Ca2+(g)	–1592	NO3–	–328
Sr2+(g)	–1445	SO42–	–1145

Lattice Dissociation Energies (`kJ/mol_(-1)`)	F–	Cl–	Br–	I–
Li+	+1031	+848	+803	+759
Na+	+918	+780	+742	+705
K+	+817	+711	+679	+651
Mg2+	+2957	+2526	+2440	+2327
Ca2+	+2630	+2258	+2176	+2074
Sr2+	+2492	+2156	+2075	+1963

Single-ion hydration energies (as shown in the table at upper right) cannot be observed directly, but are obtained from the differences in hydration energies of salts  having the given ion in common.

When you encounter tables such as the above in which numeric values are related to different elements, you should always stop and see if you can make sense of any obvious trends. In this case, the things to look for are the size and charge of the ions as they would affect the electrostatic interaction between two ions or between an ion and a [polar] water molecule.

Example 3 When calcium chloride, CaCl₂, is dissolved in water, will the temperature immediately after mixing rise or fall?

 Lattice energies are not measured directly, but are estimates based on electrostatic calculations which are reliable only for simple salts. Enthalpies of solution are observable either directly or (for sparingly soluble salts,) indirectly. Hydration energies are not measurable; they are estimated as the sum the other two quantities.

It follows that any uncertainty in the lattice energies is reflected in those of the hydration energies. For this reason, tabulated values of the latter will vary depending on the source.

As often happens for a quantity that is the sum of two large terms having opposite signs, the overall dissolution process can come out as either endothermic or exothermic, and examples of both kinds are common.

Energy terms associated with the dissolution of some salts (`kJ mol^(-1)`)
substance `=>`	LiF	NaI	KBr	CsI	LiCl	NaCl	KCl	AgCl
lattice energy	1021	682	669	586	846	778	707	910
hydration energy	1017	686	649	552	884	774	690	844
enthalpy of solution	+3	–4	+20	+34	–38	+4	+17	+66

Two common examples illustrate the contrast between exothermic and endothermic heats of solution of ionic solids:

      

Subpages (3): Example 2 Example 3 Figure 4