Entropy

Entropy

You can experience directly the mass, volume, or temperature of a substance, but you cannot experience its entropy. Consequently you may have the feeling that entropy is somehow less real than other properties of matter. We hope to show in this section that it is quite easy to predict whether the entropy under one set of circumstances will be larger than under another set of circumstances, and also to explain why. With a little practice in making such predictions in simple cases you will acquire an intuitive feel for entropy and it will lose its air of mystery.

The Third Law of Thermodynamics

The atoms, molecules, or ions that compose a chemical system can undergo several types of molecular motion, including translation, rotation, and vibration (Figure 15.3.1 "Molecular Motions"). The greater the molecular motion of a system, the greater the number of possible microstates and the higher the entropy. A perfectly ordered system with only a single microstate available to it would have an entropy of zero. The only system that meets this criterion is a perfect crystal at a temperature of absolute zero (0 K), in which each component atom, molecule, or ion is fixed in place within a crystal lattice and exhibits no motion. Such a state of perfect order (or, conversely, zero disorder) corresponds to zero entropy. In practice, absolute zero is an ideal temperature that is unobtainable, and a perfect single crystal is also an ideal that cannot be achieved. Nonetheless, the combination of these two ideals constitutes the basis for the third law of thermodynamics: the entropy of any perfectly ordered, crystalline substance at absolute zero is zero.

Figure 15.3.1 Molecular Motions

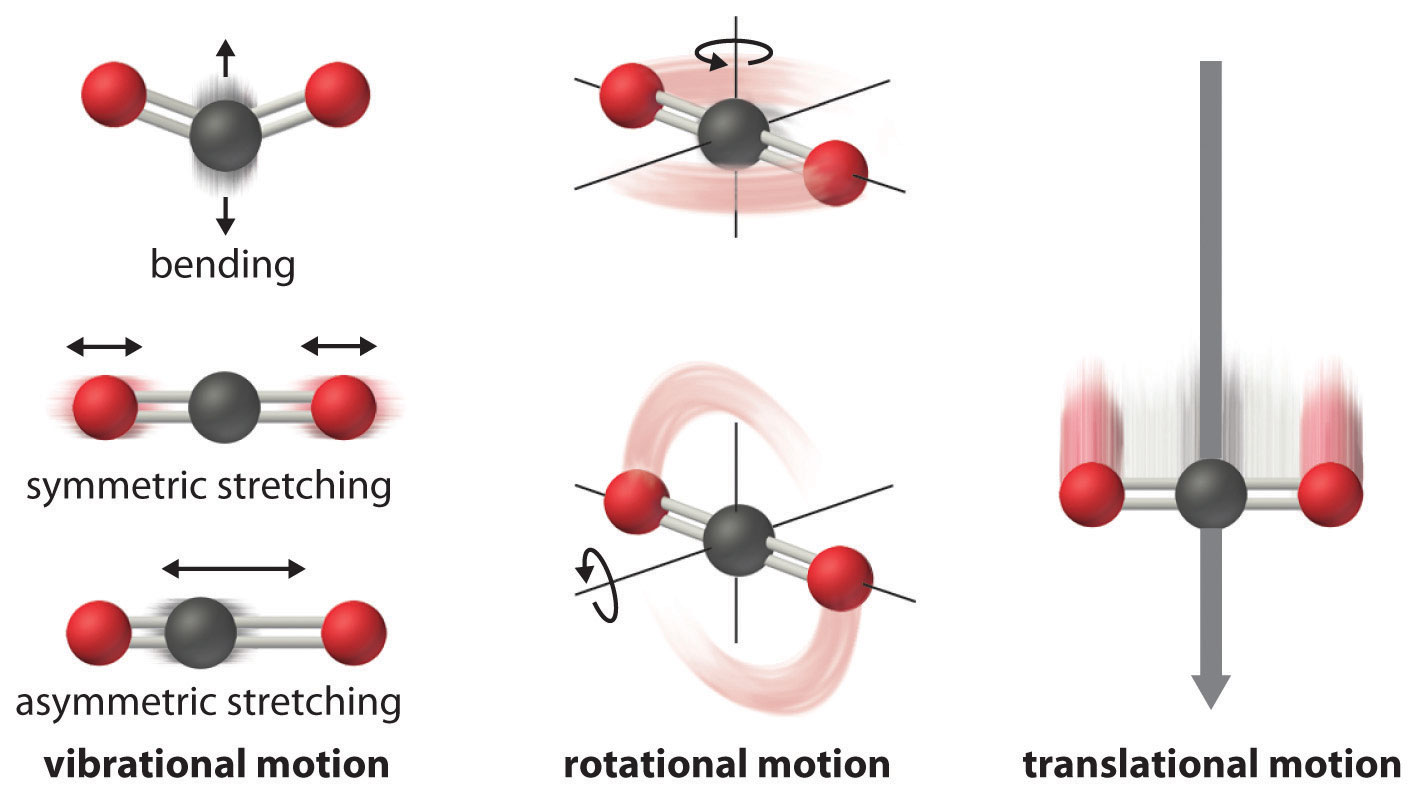
Vibrational, rotational, and translational motions of a carbon dioxide molecule are illustrated here. Only a perfectly ordered, crystalline substance at absolute zero would exhibit no molecular motion and have zero entropy. In practice, this is an unattainable ideal.

The third law of thermodynamics has two important consequences: it defines the sign of the entropy of any substance at temperatures above absolute zero as positive, and it provides a fixed reference point that allows us to measure the absolute entropy of any substance at any temperature.In practice, chemists determine the absolute entropy of a substance by measuring the molar heat capacity (C_p) as a function of temperature and then plotting the quantity C_p/T versus T. The area under the curve between 0 K and any temperature T is the absolute entropy of the substance at T. In contrast, other thermodynamic properties, such as internal energy and enthalpy, can be evaluated in only relative terms, not absolute terms. In this section, we examine two different ways to calculate ?S for a reaction or a physical change. The first, based on the definition of absolute entropy provided by the third law of thermodynamics, uses tabulated values of absolute entropies of substances. The second, based on the fact that entropy is a state function, uses a thermodynamic cycle similar to other state functions we have encountered earlier in this chapter.

The entropy of a substance depends on two things: first, the state of a substance—its temperature, pressure, and amount; and second, how the substance is structured at the molecular level. 

Temperature      As we saw in the last section, there should be only one way of arranging the energy in a perfect crystal at 0 K. If W = 1, then S = k ln W = 0; so that the entropy should be zero at the absolute zero of temperature. This rule, known as the third law of thermodynamics, is obeyed by all solids unless some randomness of arrangement is accidentally “frozen” into the crystal. As energy is fed into the crystal with increasing temperature, we find that an increasing number of alternative ways of dividing the energy between the atoms become possible. W increases, and so does S. Without exception the entropy of any pure substance always increases with temperature.

Volume and Pressure      We argued earlier that when a gas doubles its volume, the number of ways in which the gas molecules can distribute themselves in space is enormously increased and the entropy increases by 5.76 J K^–1. More generally the entropy of a gas always increases with increasing volume and decreases with increasing pressure. In the case of solids and liquids the volume changes very little with the pressure and so the entropy also changes very little.

Amount of Substance      One of the main reasons why the entropy is such a convenient quantity to use is that its magnitude is proportional to the amount of substance. Thus the entropy of 2 mol of a given substance is twice as large as the entropy of 1 mol. Properties which behave in this way are said to be extensive properties. The mass, the volume, and the enthalpy are also extensive properties, but the temperature, pressure, and thermodynamic probability are not. 

Calculating ?S from Standard Molar Entropy Values

One way of calculating ?S for a reaction is to use tabulated values of the standard molar entropy (S°), which is the entropy of 1 mol of a substance at a standard temperature of 298 K; the units of S° are J/(mol·K). Unlike enthalpy or internal energy, it is possible to obtain absolute entropy values by measuring the entropy change that occurs between the reference point of 0 K [corresponding to S = 0  J/(mol·K)] and 298 K.

As shown in Table 15.3.1 "Standard Molar Entropy Values of Selected Substances at 25°C", for substances with approximately the same molar mass and number of atoms, S° values fall in the order S°(gas) > S°(liquid) > S°(solid). For instance, S° for liquid water is 70.0 J/(mol·K), whereas S° for water vapor is 188.8 J/(mol·K). Likewise, S° is 260.7 J/(mol·K) for gaseous I₂ and 116.1 J/(mol·K) for solid I2. This order makes qualitative sense based on the kinds and extents of motion available to atoms and molecules in the three phases. The correlation between physical state and absolute entropy is illustrated in Figure 15.3.2 "A Generalized Plot of Entropy versus Temperature for a Single Substance", which is a generalized plot of the entropy of a substance versus temperature.

Table 15.3.1 Standard Molar Entropy Values of Selected Substances at 25°C

Substance	S° [J/(mol·K)]
Gases
`He`	126.2
`H_2`	130.7
`Ne`	146.3
`Ar`	154.8
`Kr`	164.1
`Xe`	169.7
`H_2O`	188.8
`N_2`	191.6
`O_2`	205.2
`CO_2`	213.8
`I_2`	260.7
Liquids
`H_2O`	70.0
CH_3OH`	126.8
`Br_2`	152.2
`CH_3CH_2OH`	160.7
`C_6H_6`	173.4
`CH_3COCl`	200.8
`C_6H_(12)` (cyclohexane)	204.4
`C_8H_(18)` (isooctane)	329.3
Solids
`C` (diamond)	2.4
`C` (graphite)	5.7
`LiF`	35.7
`SiO_2` (quartz)	41.5
`Ca`	41.6
`N`	51.3
`MgF_2`	57.2
`K`	64.7
`NaCl`	72.1
`KCl`	82.6
`I_2`	116.1

Figure 15.3.2 A Generalized Plot of Entropy versus Temperature for a Single Substance

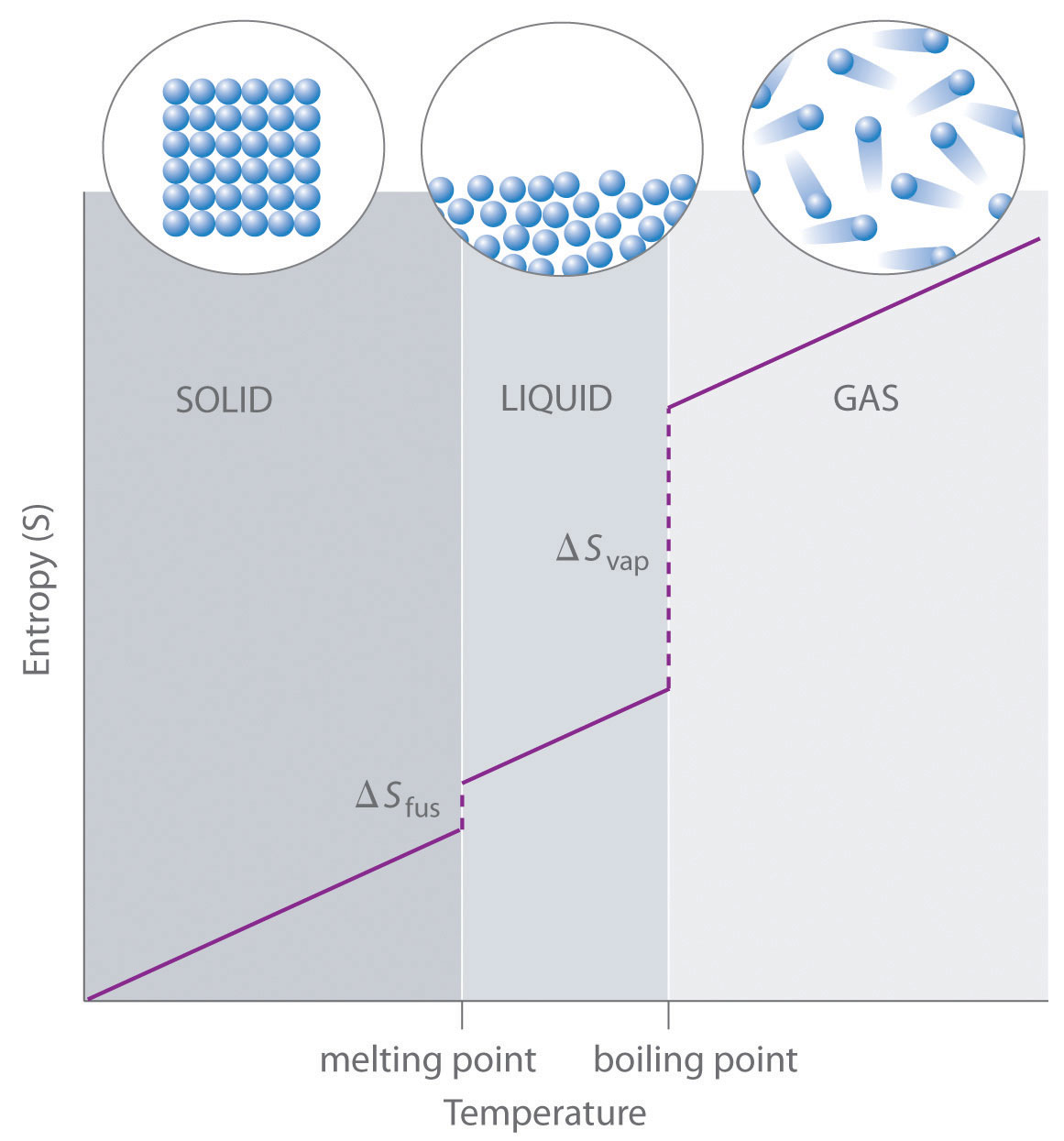
Absolute entropy increases steadily with increasing temperature until the melting point is reached, where it jumps suddenly as the substance undergoes a phase change from a highly ordered solid to a disordered liquid (?S_fus). The entropy again increases steadily with increasing temperature until the boiling point is reached, where it jumps suddenly as the liquid undergoes a phase change to a highly disordered gas (?S_vap).

A closer examination of Table 15.3.1 "Standard Molar Entropy Values of Selected Substances at 25°C" also reveals that substances with similar molecular structures tend to have similar S° values. Among crystalline materials, those with the lowest entropies tend to be rigid crystals composed of small atoms linked by strong, highly directional bonds, such as diamond [S° = 2.4 J/(mol·K)]. In contrast, graphite, the softer, less rigid allotrope of carbon, has a higher S° [5.7 J/(mol·K)] due to more disorder in the crystal. Soft crystalline substances and those with larger atoms tend to have higher entropies because of increased molecular motion and disorder. Similarly, the absolute entropy of a substance tends to increase with increasing molecular complexity because the number of available microstates increases with molecular complexity. For example, compare the S° values for CH₃OH(l) and CH₃CH₂OH(l). Finally, substances with strong hydrogen bonds have lower values of S°, which reflects a more ordered structure.

To calculate `DeltaS° ` for a chemical reaction from standard molar entropies, we use the familiar “products minus reactants” rule, in which the absolute entropy of each reactant and product is multiplied by its stoichiometric coefficient in the balanced chemical equation. Example 15.3.1 illustrates this procedure for the combustion of the liquid hydrocarbon isooctane (C₈H₁₈; 2,2,4-trimethylpentane).

Example 12

Use the data in Table 15.3.1 "Standard Molar Entropy Values of Selected Substances at 25°C" to calculate ?S° for the reaction of liquid isooctane with O₂(g) to give CO₂(g) and H₂O(g) at 298 K.

Solution:

The balanced chemical equation for the complete combustion of isooctane (`C_8H_(18)`) is as follows:

`C_8H_(18)(l) + (25)/(2))_2(g) -> 8 CO_2(g) + 9H_2 O(g)`

We calculate `DeltaS°` for the reaction using the “products minus reactants” rule, where m and n are the stoichiometric coefficients of each product and each reactant:

`DeltaS_(rxn)^° = sum mS°"(products)" - sum nS°"(reactants)"`

`=[8S°(CO_2) + 9S°(H_2O)] - [S°(C_8H_(18) + (25)/(2)S°(O_2)]`

`{[8 mol CO_2 * 213.8 J"/"(mol*K)] + [9 mo, H_2O * 188.8 J"/"(mol*K)]}`

`-{[1 mol C_8H_(18) * 329.3 J"/"(mol * K)] + [(25)/(2) mol O_2 * 205.2 J"/"(mol * K)]}`

`=515.3 J"/"K`

`DeltaS°` is positive, as expected for a combustion reaction in which one large hydrocarbon molecule is converted to many molecules of gaseous products.

2nd Law of Thermodynamics

The Second Law of Thermodynamics states that the state of entropy of the entire universe, as a closed isolated system, will always increase over time. The second law also states that the changes in the entropy in the universe can never be negative. 

The second law states that the entropy of the universe (not necessarily the system) increases during a spontaneous process, that is,

`DeltaS_"universe"=DeltaS_"system"+DeltaS_"surroundings" > 0 `(during a spontaneous process)

Subpages (1): Example 12