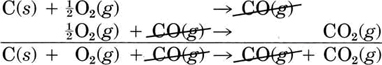Hess's Law

Perhaps the most useful feature of thermochemical equations is that they can be combined to determine ?H_m values for other chemical reactions. Consider, for example, the following two-step sequence. Step 1 is reaction of 1 mol C(s) and 0.5 mol O₂(g) to form 1 mol CO(g):

`C(s) + (1/2)O_2(g) -> CO(g)`      `DeltaH_m = –110.5 kJ = DeltaH_1`

(Note that since the equation refers to moles, not molecules, fractional coefficients are permissible.) In step 2 the mole of `CO` reacts with an additional 0.5 mol `O_2` yielding 1 mol `CO_2`:

`CO(g) + (1/2)O_2(g) -> CO_2(g)`      `DeltaH_m = –283.0 kJ = DeltaH_2`

The net result of this two-step process is production of 1 mol `CO_2` from the original 1 mol `C` and 1 mol `O_2` (0.5 mol in each step). All the `CO` produced in step 1 is used up in step 2.

On paper this net result can be obtained by adding the two chemical equations as though they were algebraic equations. The `CO` produced is canceled by the `CO` consumed since it is both a reactant and a product of the overall reaction

Experimentally it is found that the enthalpy change for the net reaction is the sum of the enthalpy changes for steps 1 and 2:

`DeltaH_"net" = –110.5 kJ + (–283.0 kJ) = –393.5 kJ = DeltaH_1 + DeltaH_2`

That is, the thermochemical equation

`C(s) + O_2(g) -> CO_2(g)`      `DeltaH_m = –393.5 kJ`

is the correct one for the overall reaction.

In the general case it is always true that whenever two or more chemical equations can be added algebraically to give a net reaction, their enthalpy changes may also be added to give the enthalpy change of the net reaction.

This principle is known as Hess' law. If it were not true, it would be possible to think up a series of reactions in which energy would be created but which would end up with exactly the same substances we started with. This would contradict the law of conservation of energy. Hess’ law enables us to obtain `DeltaH_m` values for reactions which cannot be carried out experimentally, as the next example shows.

EXAMPLE 10 Acetylene (`C_2H_2`) cannot be prepared directly from its elements according to the equation

`2C(s) + H_2(g) -> C_2H_2(g)`      (1)

Calculate `DeltaH_m` for this reaction from the following thermochemical equations, all of which can be determined experimentally:

`C(s) + O_2(g) -> CO_2(g)`      `DeltaH_m = –393.5 kJ`  (2a)

`H_2(g) + (1/2)O_2(g) -> H_2O(l)`      `DeltaH_m = –285.8 kJ`   (2b)

`C_2H_2(g) + 5/2 O_2(g) -> 2CO_2(g) + H_2O(l)`      `DeltaH_m = –1299.8 kJ`    (2c) 

We use the following strategy to manipulate the three experimental equations so that when added they yield Eq. (1):

a) Since Eq. (1) has 2 mol `C` on the left, we multiply Eq. (2a) by 2.

b) Since Eq. (1) has 1 mol `H_2` on the left, we leave Eq. (2b) unchanged.

c) Since Eq. (1) has 1 mol `C_2H_2` on the right, whereas there is 1 mol `C_2H_2` on the left of Eq. (2c) we write Eq. (2c) in reverse.

We then have

`2C(s) + 2 O_2 (g) -> 2CO_2(g)`     `DeltaH_m = 2(-393.5) kJ`

`H_2 (g) + 1/2 O_2 (g) -> H_2 O(l)`     `DeltaH_m = -285.8 kJ`

`2 CO_2 (g) + H_2 O(l) -> C_2H_2 (g) + 5/2 O_2 (g)`     `DeltaH_m = -(-1299.8 kJ)`

`=`

`2C(s) + H_2 (g) + 2(1/2)O_2 (g) -> C_2H_2 (g) + (5/2) O_2 (g)`

Cancelling the `(5"/"2) O_2` on each side, we get:

`2C(s) + H_2 (g) -> C_2H_2 (g)`      `DeltaH_m = 227.0 kJ`

Subpages (1): Example 10